
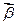 =
=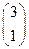 ,变换T的矩阵为A=
,变换T的矩阵为A=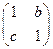 ,平面上的点P(1,1)在变换T
,平面上的点P(1,1)在变换T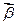 .
.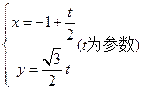 与圆
与圆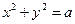 (
(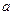 >0)相交于A、B两点,设
>0)相交于A、B两点,设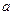 的值
的值
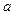 2+
2+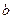 2恒成立,试求2
2恒成立,试求2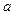 +
+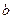 的最大值。
的最大值。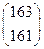 .
.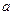 =3.
=3.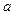 +
+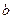 )max=
)max=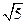 .
.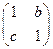
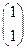 =
=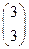 即
即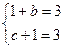

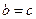 =2,
=2,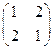 . ------------------------------------ 2分
. ------------------------------------ 2分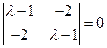


 λ1=-1,λ2="3."
λ1=-1,λ2="3." 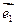 =
=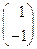 .
.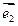 =
=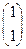 . -----------------------------4分
. -----------------------------4分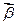 =A4(
=A4(
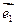 +2
+2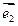 )
)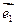 +2A4
+2A4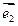
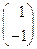 +2·34
+2·34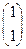
 . -
. - -----------------------------------7分
-----------------------------------7分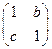
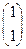 =
=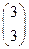 ,
,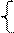
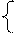 即
即 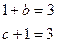

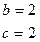 ,
,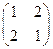 . ------------------------------------2分
. ------------------------------------2分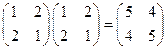 ,
,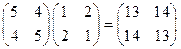 ,
,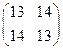
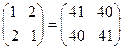 , ------------------------------------5分
, ------------------------------------5分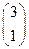 =
=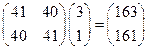 . -----------------------------------7分
. -----------------------------------7分 置关系,考查运算求解能力.
置关系,考查运算求解能力.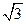 (x+1) --------------------------------1分
(x+1) --------------------------------1分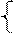 联立方程
联立方程  ,
,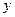 ,得:4
,得:4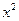 +6
+6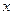 +3-r="0" . ------------------------------------2分
+3-r="0" . ------------------------------------2分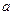 )>0 , …………①
)>0 , …………①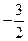 , …………②
, …………②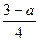 , …………③-----------------------------------3分
, …………③-----------------------------------3分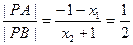 , …………④-----------------------------------5分
, …………④-----------------------------------5分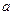 ="3. " -----------------------------------7分
="3. " -----------------------------------7分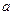 ="0 " -----------------------------------1分
="0 " -----------------------------------1分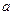 )
) >0
>0 
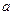 >
> .
. 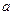 .…………(*)-----------------------------------3分
.…………(*)-----------------------------------3分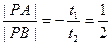 或
或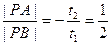 . ---------------------------5分
. ---------------------------5分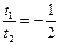 ,解得
,解得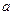 =3,
=3,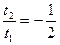 ,代入(*)得
,代入(*)得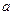 =
= 3,
3,
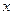 -1|+|
-1|+|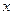 -2|=|
-2|=|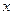 -1|+|2-
-1|+|2-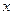 |≥|
|≥|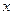 -1+2-
-1+2-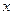 |="1" , -------------2分
|="1" , -------------2分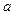 2+
2+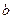 2≤1.
2≤1.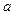 +
+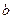 )2≤(22+12)(
)2≤(22+12)( 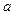 2+
2+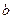 2) ≤5. ---------------------------------4分
2) ≤5. ---------------------------------4分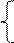
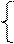 由
由 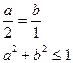
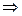
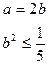 ,
,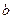 =
=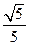 ,
,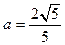 时等号成立. --------------------------------6分
时等号成立. --------------------------------6分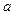 +
+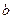 )max=
)max=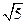 . -----------------------------------7分
. -----------------------------------7分

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源:不详 题型:解答题
 ,N=
,N=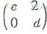 ,且MN=
,且MN=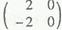 。
。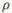 =2
=2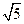 sin
sin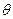 。
。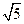 ),求∣PA∣+∣PB∣。
),求∣PA∣+∣PB∣。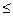 3的解集为
3的解集为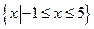 ,求实数a的值;
,求实数a的值;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

|






 学科
学科 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
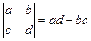 ,则符合条件
,则符合条件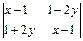 = 0的点P (x , y)的轨迹方程为( )
= 0的点P (x , y)的轨迹方程为( )| A.(x – 1)2 + 4y2 =" 1" | B.(x –1)2 – 4y2 =" 1" |
| C.(x –1)2 + y2 =" 1" | D.(x –1)2 – y2 = 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com