
【题目】已知 ![]() ,其中a>0,a≠1.
,其中a>0,a≠1.
(Ⅰ)若f(x)在(﹣∞,+∞)上是单调函数,求实数a,b的取值范围;
(Ⅱ)当a=2时,函数f(x)在(﹣∞,+∞)上只有一个零点,求实数b的取值范围.
【答案】解:(Ⅰ)∵f(x)在(﹣∞,+∞)上是单调函数,且在(﹣∞,0)上递增,
∴f(x)在[0,+∞)上是递增函数∴a>1,且f(0)=1+b≥﹣1,得b≥﹣2,
∴a>1,b≥﹣2.
(Ⅱ)∵x<0时,f(x)<﹣1,∴f(x)在(﹣∞,0)上无零点,
∴x≥0时,f(x)=2x+b只有一个零点,
∵f(x)在[0,+∞)递增,
∴f(0)=1+b≤0,即b≤﹣1.
∴实数b的取值范围是b∈(﹣∞,﹣1]
【解析】(Ⅰ)由题意可得出f(x在(﹣∞,0)上递增,f(x)在[0,+∞)上是也递增函数,根据指数函数的单调性可得到a>1,再根据二次函数的单调性得出f(0)≥﹣1,即得出b≥﹣2。(Ⅱ)当a=2时,由∵x<f(x)<﹣1可得到f(x)在(﹣∞,0)上无零点,所以当x≥0时,f(x)=2x+b只有一个零点,再根据函数的增减性得出b≤﹣1.


科目:高中数学 来源: 题型:
【题目】某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,80件,60件.为了解它们的产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为n的样本进行调查,其中从丙车间的产品中抽取了3件,则n=( )
A.9
B.10
C.12
D.13
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=f(x)是定义域为R的偶函数,且在(0,+∞)上单调递减,则( )
A.f(﹣π)>f(﹣1)>f( ![]() )
)
B.f(﹣1)>f(﹣π)>f( ![]() )
)
C.f(﹣π)>f( ![]() )>f(﹣1)
)>f(﹣1)
D.f(﹣1)>f( ![]() )>f(﹣π)
)>f(﹣π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知指数函数y=ax(a>0,且a≠1)的图象过点(1, ![]() ).
).
(I)求函数y=f(x)的解析式;
II)若不等式满足f(2x+1)>1,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足:a3=7,a5+a7=26.{an}的前n项和为Sn . (Ⅰ)求an及Sn;
(Ⅱ)令bn= ![]() (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m、n、s、t∈R* , m+n=3, ![]() 其中m、n是常数且m<n,若s+t的最小值 是
其中m、n是常数且m<n,若s+t的最小值 是 ![]() ,满足条件的点(m,n)是椭圆
,满足条件的点(m,n)是椭圆 ![]() 一弦的中点,则此弦所在的直线方程为( )
一弦的中点,则此弦所在的直线方程为( )
A.x﹣2y+3=0
B.4x﹣2y﹣3=0
C.x+y﹣3=0
D.2x+y﹣4=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,一个矩形花园里需要铺两条笔直的小路,已知矩形花园长AD=5m,宽AB=3m,其中一条小路定为AC,另一条小路过点D,问如何在BC上找到一点M,使得两条小路AC与DM相互垂直?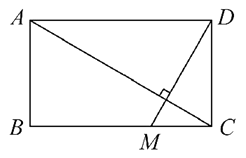
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】咖啡馆配制两种饮料,甲种饮料每杯分别用奶粉、咖啡、糖9g、4g、3g;乙种饮料每杯分别用奶粉、咖啡、糖4g、5g、10g,已知每天使用原料限额为奶粉3600g,咖啡2000g,糖3000g,如果甲种饮料每杯能获利0.7元,乙种饮料每杯能获利1.2元,每天在原料使用的限额内,饮料能全部售完,问咖啡馆每天怎样安排配制饮料获利最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com