
【题目】已知函数f(x)=(x2+bx+b) ![]() (b∈R)
(b∈R)
(1)当b=4时,求f(x)的极值;
(2)若f(x)在区间(0, ![]() )上单调递增,求b的取值范围.
)上单调递增,求b的取值范围.
【答案】
(1)解:当b=4时,f(x)=(x2+4x+4) ![]() =
= ![]() (x
(x ![]() ),
),
则 ![]() =
= ![]() .
.
由f′(x)=0,得x=﹣2或x=0.
当x<﹣2时,f′(x)<0,f(x)在(﹣∞,﹣2)上为减函数.
当﹣2<x<0时,f′(x)>0,f(x)在(﹣2,0)上为增函数.
当0<x< ![]() 时,f′(x)<0,f(x)在(0,
时,f′(x)<0,f(x)在(0, ![]() )上为减函数.
)上为减函数.
∴当x=﹣2时,f(x)取极小值为0.
当x=0时,f(x)取极大值为4
(2)解:由f(x)=(x2+bx+b) ![]() ,得:
,得:
![]()
![]()
= ![]() .
.
由f(x)在区间(0, ![]() )上单调递增,
)上单调递增,
得f′(x)≥0对任意x∈(0, ![]() )恒成立.
)恒成立.
即﹣5x2﹣3bx+2x≥0对任意x∈(0, ![]() )恒成立.
)恒成立.
∴ ![]() 对任意x∈(0,
对任意x∈(0, ![]() )恒成立.
)恒成立.
∵ ![]() .
.
∴ ![]() .
.
∴b的取值范围是 ![]()
【解析】(1)把b=4代入函数解析式,求出函数的导函数,由导函数的零点对定义域分段,由导函数在各区间段内的符号判断原函数的单调性,从而求得极值;(2)求出原函数的导函数,由导函数在区间(0, ![]() )上大于等于0恒成立,得到
)上大于等于0恒成立,得到 ![]() 对任意x∈(0,
对任意x∈(0, ![]() )恒成立.由单调性求出
)恒成立.由单调性求出 ![]() 的范围得答案.
的范围得答案.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程![]()
(3)试预测加工10个零件需要多少小时?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数
f(x)=(cosx﹣x)(π+2x)﹣ ![]() (sinx+1)
(sinx+1)
g(x)=3(x﹣π)cosx﹣4(1+sinx)ln(3﹣ ![]() )
)
证明:
(1)存在唯一x0∈(0, ![]() ),使f(x0)=0;
),使f(x0)=0;
(2)存在唯一x1∈( ![]() ,π),使g(x1)=0,且对(Ⅰ)中的x0 , 有x0+x1<π.
,π),使g(x1)=0,且对(Ⅰ)中的x0 , 有x0+x1<π.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机将1,2,…,2n(n∈N* , n≥2)这2n个连续正整数分成A、B两组,每组n个数,A组最小数为a1 , 最大数为a2;B组最小数为b1 , 最大数为b2;记ξ=a2﹣a1 , η=b2﹣b1 .
(1)当n=3时,求ξ的分布列和数学期望;
(2)C表示事件“ξ与η的取值恰好相等”,求事件C发生的概率P(C);
(3)对(2)中的事件C, ![]() 表示C的对立事件,判断P(C)和P(
表示C的对立事件,判断P(C)和P( ![]() )的大小关系,并说明理由.
)的大小关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,且椭圆
,且椭圆![]() 上一点
上一点![]() 到点
到点![]() 的距离的最大值为
的距离的最大值为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() ,
, ![]() 为抛物线
为抛物线![]() :
: ![]() 上一动点,过点
上一动点,过点![]() 作抛物线
作抛物线![]() 的切线交椭圆
的切线交椭圆![]() 于
于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆C:![]() (a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知椭圆C的离心率为
(a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知椭圆C的离心率为![]() ,且经过点(0,1).
,且经过点(0,1).
(1)求实数a,b的值;
(2)若过点P(0,m)(m>0)的直线l与椭圆C有且只有一个公共点,且l被椭圆C的伴随圆C1所截得的弦长为2![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在一个矩形污水处理池![]() 的池底水平铺设污水净化管道(
的池底水平铺设污水净化管道(![]() ,
,![]() 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口![]() 是
是![]() 的中点,
的中点,![]() 分别落在线段
分别落在线段![]() 上.已知
上.已知![]() 米,
米,![]() 米,记
米,记![]() .
.
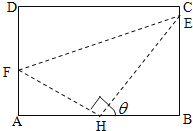
(1)试将污水净化管道的长度![]() 表示为
表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)若![]() ,求此时管道的长度
,求此时管道的长度![]() ;
;
(3)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度.
取何值时,污水净化效果最好?并求出此时管道的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com