
【题目】对函数![]() (其中
(其中![]() 为实数,
为实数,![]() ),给出下列命题;
),给出下列命题;
①当![]() 时,
时,![]() 在定义域上为单调递减函数;②对任意
在定义域上为单调递减函数;②对任意![]() ,
,![]() 都不是奇函数;③当
都不是奇函数;③当![]() 时,
时,![]() 为偶函数;④关于
为偶函数;④关于![]() 的方程
的方程![]() 最多有一个实数根,其中正确命题的序号为________,(把所有正确的命题序号写入横线)
最多有一个实数根,其中正确命题的序号为________,(把所有正确的命题序号写入横线)
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
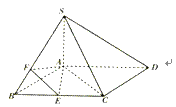
【题目】如图所示,四棱锥S﹣ABCD中,四边形ABCD为平行四边形,BA⊥AC,SA⊥AD,SC⊥CD.
(Ⅰ)求证:AC⊥SB;
(Ⅱ)若AB=AC=SA=3,E为线段BC的中点,F为线段SB上靠近B的三等分点,求直线SC与平面AEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016高考新课标II,理15)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,椭圆上动点P到一个焦点的距离的最小值为3(
,椭圆上动点P到一个焦点的距离的最小值为3(![]() -1).
-1).
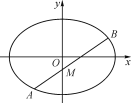
(1) 求椭圆C的标准方程;
(2) 已知过点M(0,-1)的动直线l与椭圆C交于A,B两点,试判断以线段AB为直径的圆是否恒过定点,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com