
【题目】已知函数![]() .
.
(1)当![]() 时,试求
时,试求![]() 的单调区间;
的单调区间;
(2)若![]() 在
在![]() 内有极值,试求
内有极值,试求![]() 的取值范围.
的取值范围.
【答案】(1)单调增区间为(1,+∞),单调减区间为(0,1);(2)a∈(e,+∞)
【解析】
(1)首先求得![]() 定义域为
定义域为![]() ,求导后,通过证明
,求导后,通过证明![]() 恒成立可知导函数符号由
恒成立可知导函数符号由![]() 的符号决定,从而可求得函数的单调区间;(2)将
的符号决定,从而可求得函数的单调区间;(2)将![]() 在
在![]() 内有极值转化为
内有极值转化为![]() 在
在![]() 内有零点,即
内有零点,即![]() 有解,令
有解,令![]() ,
,![]() ,利用导数可求得
,利用导数可求得![]() ,从而可验证出
,从而可验证出![]() 时
时![]() 在
在![]() 内有零点,从而得到结果.
内有零点,从而得到结果.
(1)由题意知,![]() 定义域为:
定义域为:![]()
当![]() 时,
时,![]()
则:![]()
令![]() ,则
,则![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 在
在![]() 上单调递减;在
上单调递减;在![]() 上单调递增
上单调递增 ![]()
即:对任意的![]() ,
,![]() 恒成立
恒成立
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 的单调递增区间为:
的单调递增区间为:![]() ;单调递减区间为:
;单调递减区间为:![]()
(2)若![]() 在
在![]() 内有极值,则
内有极值,则![]() 在
在![]() 内有零点
内有零点
由![]() ,得:
,得:![]() ,则
,则![]()
设![]() ,
,![]() ,则
,则![]() 恒成立
恒成立
![]() 在
在![]() 上单调递减
上单调递减 ![]()
当![]() 时,
时,![]() 在
在![]() 内有解
内有解
设![]() ,则
,则![]()
当![]() 时,
时,![]()
![]() 在
在![]() 上单调递减
上单调递减
又![]() ,
,![]()
![]() 在
在![]() 上有唯一解
上有唯一解![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 当
当![]() 时,
时,![]() 在
在![]() 内有唯一极值
内有唯一极值
当![]() 时,
时,![]() 在
在![]() 上单调递增,不存在极值
上单调递增,不存在极值
综上所述:![]()


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 过点
过点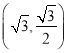 ,左右焦点为
,左右焦点为![]() ,且椭圆C关于直线
,且椭圆C关于直线![]() 对称的图形过坐标原点。
对称的图形过坐标原点。
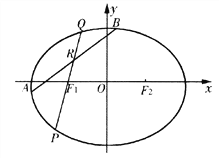
(I)求椭圆C方程;
(II)圆D: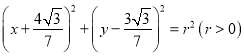 与椭圆C交于A,B两点,R为线段AB上任一点,直线F1R交椭圆C于P,Q两点,若AB为圆D的直径,且直线F1R的斜率大于1,求
与椭圆C交于A,B两点,R为线段AB上任一点,直线F1R交椭圆C于P,Q两点,若AB为圆D的直径,且直线F1R的斜率大于1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
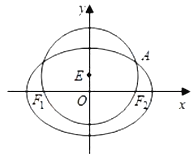
【题目】已知圆![]() :
: ![]() 经过椭圆
经过椭圆![]() :
: ![]() 的左右焦点
的左右焦点![]() ,且与椭圆
,且与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() 三点共线,直线
三点共线,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,且
两点,且![]() (
(![]() ).
).
(1)求椭圆![]() 的方程;
的方程;
(2)当三角形![]() 的面积取得最大值时,求直线
的面积取得最大值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂拟建一座平面图(如右图所示)为矩形且面积为200平方米的三级污水处理池,由于地形限制,长、宽都不能超过16米,如果池外周壁建造单价为每米400元,中间两条隔墙建造单价为每米248元,池底建造单价为每平方米80元(池壁厚度忽略不计,且池无盖).

(1)写出总造价y(元)与污水处理池长x(米)的函数关系式,并指出其定义域;
(2)求污水处理池的长和宽各为多少时,污水处理池的总造价最低?并求最低总造价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点
的右焦点![]() ,过点
,过点![]() 且与坐标轴不垂直的直线与椭圆交于
且与坐标轴不垂直的直线与椭圆交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 经过椭圆的一个顶点时其倾斜角恰好为
经过椭圆的一个顶点时其倾斜角恰好为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,线段
为坐标原点,线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知棱锥P-ABC 中.PA⊥平面ABC,AB⊥AC,PA=AC=![]() AB=1,N为AB 上一点,AB=4AN,M.S分别为PB,BC的中点.
AB=1,N为AB 上一点,AB=4AN,M.S分别为PB,BC的中点.
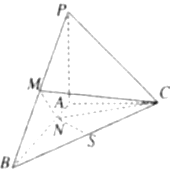
(1)证明:CM⊥SN;
(2)求二面角M-NC-B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A是圆O:x2+y2=16上的任意一点,l是过点A且与x轴垂直的直线,B是直线l与x轴的交点,点Q在直线l上,且满足4|BQ|=3|BA|.当点A在圆O上运动时,记点Q的轨迹为曲线C.
(1)求曲线C的方程;
(2)已知直线y=kx﹣2(k≠0)与曲线C交于M,N两点,点M关于y轴的对称点为M′,设P(0,﹣2),证明:直线M′N过定点,并求△PM′N面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 分别是椭圆C:
分别是椭圆C:![]() 的左、右焦点,
的左、右焦点,![]() ,直线1过
,直线1过![]() 且垂直于x轴,交椭圆C于A、B两点,连接A、B、
且垂直于x轴,交椭圆C于A、B两点,连接A、B、![]() ,所组成的三角形为等边三角形。
,所组成的三角形为等边三角形。
(1)求椭圆C的方程;
(2)过右焦点![]() 的直线m与椭圆C相交于M、N两点,试问:椭圆C上是否存在点P,使
的直线m与椭圆C相交于M、N两点,试问:椭圆C上是否存在点P,使![]() 成立?若存在,求出点P的坐标;若不存在,说明理由.
成立?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com