
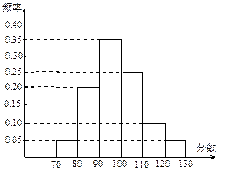
科目:高中数学 来源:不详 题型:解答题
 分配相应的低息贷款金额,其评估标准和贷款金额如下表:
分配相应的低息贷款金额,其评估标准和贷款金额如下表:| 评估得分 | [50,60) | [60,70) | [70,80) | [80,90] |
| 评定类型 | 不合格 | 合格 | 良好 | 优秀 |
| 贷款金额(万元) | 0 | 200 | 400 | 800 |
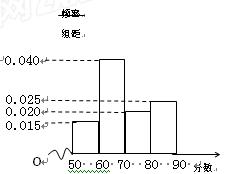
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.两个变量的线性相关关系越强 | B.两个变量的线性相关关系越弱 |
| C.回归模型的拟合效果越好 | D.回归模型的拟合效果越差 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 在去年的国际联赛
在去年的国际联赛 中,甲队平均每场进球数为3.2,全年比赛
中,甲队平均每场进球数为3.2,全年比赛 进球个数的标准差为3;乙队平均每场进球数为
进球个数的标准差为3;乙队平均每场进球数为 1.8,全年比赛进球数个数的标准差是0.3,下列说法中正确的个数为( )
1.8,全年比赛进球数个数的标准差是0.3,下列说法中正确的个数为( )| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| | 优秀 | 不优秀 | 合计 |
| 甲班 | 10 | 35 | 45 |
| 乙班 | 7 | 38 | 45 |
| 合计 | 17 | 73 | 90 |
A.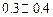 | B.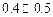 | C.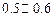 | D.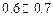 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.卡方独立性检验的统计假设是各事件之间相互独立 | B.卡方的值可以为负值 | C.卡方独立性检验显示“患慢性气管炎和吸烟习惯有关”即指“有吸烟习惯的人必会患慢性气管炎” | D. 2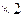 列联表中的4个数据可为任何实数 列联表中的4个数据可为任何实数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com