练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）=|log0.5x|，若正实数m，n（m＜n）满足f（m）=f（n），且f（x）在区间[m2 ， n]上的最大值为4，则n﹣m=（ ）
    A.
    B.
    C.
    D.

    【答案】B
    【解析】解：∵f（x）=|log0.5x|，正实数m，n（m＜n）满足f（m）=f（n），
    ∴0＜m＜1＜n，且|log0.5m|=|log0.5n|，∴log0.5m=﹣log0.5n，
    ∴log0.5m+log0.5n=0，解得mn=1，
    又∵f（x）在区间[m2 ， n]上的最大值为4，
    ∴|log0.5m2|=4或|log0.5n|=4，即log0.5m2=4或log0.5n=﹣4，
    解得m= 或n=16，当m= 时，由mn=1可得n=4，此时n﹣m= ；
    当n=16时，由mn=1可得m= ，这与m＜n矛盾，应舍去．
    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数是定义在上的奇函数，且当时， ，则对任意，函数的零点个数至多有（ ）

    A. 3个 B. 4个 C. 6个 D. 9个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若正实数a，b满足a+b=1，则（ ）
    A. 有最大值4
    B.ab有最小值
    C. 有最大值
    D.a2+b2有最小值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在正方体ABCD﹣A1B1C1D1中，S是B1D1的中点，E，F，G分别是BC，CD和SC的中点．求证：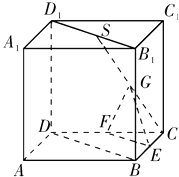

    （1）直线EG∥平面BDD1B1；
    （2）平面EFG∥平面BDD1B1 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，是函数y=f（x）的导函数f′（x）的图象，则下面判断正确的是（ ）

    A.在区间（﹣2，1）上f（x）是增函数
    B.在（1，3）上f（x）是减函数
    C.在（4，5）上f（x）是增函数
    D.当x=4时，f（x）取极大值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知θ∈（ ， ），若存在实数x，y同时满足 = ， + = ，则tanθ的值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】椭圆E经过点A（2，3），对称轴为坐标轴，焦点F1 ， F2在x轴上，离心率e= ．

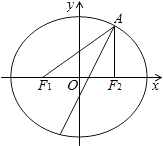
    （1）求椭圆E的方程；
    （2）求∠F1AF2的角平分线所在直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某保险公司研究一款畅销保险产品的保费与销量之间的关系，根据历史经验，若每份保单的保费在元的基础上每增加元，对应的销量（万份）与（元）有较强线性相关关系，从历史销售记录中抽样得到如下组与的对应数据：

    （1）试据此求出关于的线性回归方程；

    （2）若把回归方程当做与的线性关系，试计算每份保单的保费定为多少元此产品的保费总收入最大，并求出该最大值；

    参考公式：

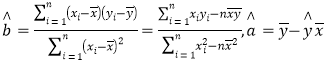
    参考数据：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】平面直角坐标系xOy中，A（2，4），B（﹣1，2），C，D为动点，
    （1）若C（3，1），求平行四边形ABCD的两条对角线的长度
    （2）若C（a，b），且 ，求 取得最小值时a，b的值．

    查看答案和解析>>

    同步练习册答案