
本小题共13分)
对数列 ,规定
,规定 为数列
为数列 的一阶差分数列,其中
的一阶差分数列,其中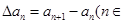 N*).对正整数k,规定
N*).对正整数k,规定  为
为 的k阶差分数列,其中
的k阶差分数列,其中
 .
.
(Ⅰ)若数列 的首项
的首项 ,且满足
,且满足 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅱ)对(Ⅰ)中的数列 ,若数列
,若数列 是等差数列,使得
是等差数列,使得
 对一切正整数
对一切正整数 N*都成立,求
N*都成立,求 ;
;
(Ⅲ) 在(Ⅱ)的条件下,令 设
设 若
若 成立,求最小正整数
成立,求最小正整数 的值.
的值.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
(本小题共13分)
一厂家向用户提供的一箱产品共10件,其中有2件次品,用户先对产品进行抽检以决定是否接收。抽检规定是这样的:一次取一件产品检查,若前三次没有抽查到次品,则用户接收这箱产品,而前三次中只要抽查到次品就停止抽检,并且用户拒绝接收这箱产品。
(I)求这箱产品被用户拒绝接收的概率;
(II)记![]() 表示抽检的产品件数,求
表示抽检的产品件数,求![]() 的概率分布列。
的概率分布列。
查看答案和解析>>
科目:高中数学 来源:2010年北京市崇文区高三下学期一模数学(文)测试 题型:解答题
(本小题共13分)
已知数列 的前
的前 项和为
项和为 ,且
,且 .
.
数列 满足
满足 (
( ),且
),且 ,
, .
.
(Ⅰ)求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)设 ,数列
,数列 的前
的前 项和为
项和为 ,求使不等式
,求使不等式 对一切
对一切 都成立的最大正整数
都成立的最大正整数 的值;
的值;
(Ⅲ)设 是否存在
是否存在 ,使得
,使得 成立?若存在,求出
成立?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2010年北京市宣武区高三第二次模拟考试数学(理) 题型:解答题
(本小题共13分)[来源:Z,xx,k.Com]
在一次考试中共有8道选择题,每道选择题都有4个选项,其中有且只有一个选项是正确的.某考生有4道题已选对正确答案,其余题中有两道只能 分别判断2个选项是错误的,还有两道题因不理解题意只好乱猜.
分别判断2个选项是错误的,还有两道题因不理解题意只好乱猜.
(Ⅰ) 求该考生8道题全答对的概率;
(Ⅱ)
若评分标准规定:“每题只选一个选项,选对得5分,不选或选错得0分”,求该考生所得分数的分布列.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市高三压轴文科数学试卷(解析版) 题型:解答题
(本小题共13分)
已知向量 ,设函数
,设函数 .
.
(Ⅰ)求函数 在
在 上的单调递增区间;
上的单调递增区间;
(Ⅱ)在 中,
中, ,
, ,
, 分别是角
分别是角 ,
, ,
, 的对边,
的对边, 为锐角,若
为锐角,若 ,
, ,
, 的面积为
的面积为 ,求边
,求边 的长.
的长.
查看答案和解析>>
科目:高中数学 来源:2011年普通高中招生考试北京市高考理科数学 题型:解答题
((本小题共13分)
若数列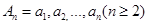 满足
满足 ,数列
,数列 为
为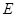 数列,记
数列,记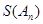 =
= .
.
(Ⅰ)写出一个满足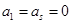 ,且
,且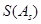 〉0的
〉0的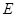 数列
数列 ;
;
(Ⅱ)若 ,n=2000,证明:E数列
,n=2000,证明:E数列 是递增数列的充要条件是
是递增数列的充要条件是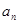 =2011;
=2011;
(Ⅲ)对任意给定的整数n(n≥2),是否存在首项为0的E数列 ,使得
,使得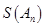 =0?如果存在,写出一个满足条件的E数列
=0?如果存在,写出一个满足条件的E数列 ;如果不存在,说明理由。
;如果不存在,说明理由。
【解析】:(Ⅰ)0,1,2,1,0是一具满足条件的E数列A5。
(答案不唯一,0,1,0,1,0也是一个满足条件的E的数列A5)
(Ⅱ)必要性:因为E数列A5是递增数列,所以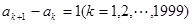 .所以A5是首项为12,公差为1的等差数列.所以a2000=12+(2000—1)×1=2011.充分性,由于a2000—a1000
.所以A5是首项为12,公差为1的等差数列.所以a2000=12+(2000—1)×1=2011.充分性,由于a2000—a1000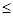 1,a2000—a1000
1,a2000—a1000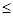 1……a2—a1
1……a2—a1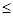 1所以a2000—a
1所以a2000—a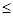 19999,即a2000
19999,即a2000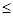 a1+1999.又因为a1=12,a2000=2011,所以a2000=a1+1999.故
a1+1999.又因为a1=12,a2000=2011,所以a2000=a1+1999.故 是递增数列.综上,结论得证。
是递增数列.综上,结论得证。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com