Question

设函数f(x)对所有的实数x都满足f(x+2π)=f(x)，求证：存在4个函数f_i(x)(i=1，2，3，4)满足：（1）对i=1，2，3，4，f_i(x)是偶函数，且对任意的实数x，有f_i(x+π)=f_i(x)；（2）对任意的实数x，有f(x)=f₁(x)+f₂(x)cosx+f₃(x)sinx+f₄(x)sin2x。

Answer 1

证明略

解析:

记，，则f(x)=g(x)+h(x)，且g(x)是偶函数，h(x)是奇函数，对任意的x∈R，g(x+2π)=g(x)，h(x+2π)=h(x)。令，，，

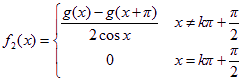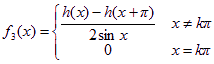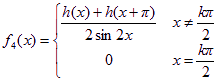，其中k为任意整数。

容易验证f_i(x)，i=1，2，3，4是偶函数，且对任意的x∈R，f_i(x+π)=f_i(x)，i=1，2，3，4。下证对任意的x∈R，有f₁(x)+f₂(x)cosx=g(x)。当时，显然成立；当时，因为，而

，故对任意的x∈R，f₁(x)+f₂(x)cosx=g(x)。

下证对任意的x∈R，有f₃(x)sinx+f₄(x)sin2x=h(x)。当时，显然成立；当x=kπ时，h(x)=h(kπ)=h(kπ-2kπ)=h(-kπ)=-h(kπ)，所以h(x)=h(kπ)=0，而此时f₃(x)sinx+f₄(x)sin2x=0，故h(x)=f₃(x)sinx+f₄(x)sin2x；当时，

，故，又f₄(x)sin2x=0，从而有h(x)=f₃(x)sinx+f₄(x)sin2x。

于是，对任意的x∈R，有f₃(x)sinx+f₄(x)sin2x=h(x)。综上所述，结论得证。