
【题目】如图,以![]() ,
,![]() 为顶点作正三角形
为顶点作正三角形![]() ,再以
,再以![]() 和
和![]() 的中点
的中点![]() 为顶点作正三角形
为顶点作正三角形![]() ,再以
,再以![]() 和
和![]() 的中点
的中点![]() 为顶点作正三角形
为顶点作正三角形![]() ,
,![]() ,如此继续下去.有如下结论:
,如此继续下去.有如下结论:

①所作的正三角形的边长构成公比为![]() 的等比数列;
的等比数列;
②每一个正三角形都有一个顶点在直线![]() 上;
上;
③第六个正三角形的不在第五个正三角形边上的顶点![]() 的坐标是
的坐标是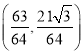 ;
;
④第![]() 个正三角形的不在第
个正三角形的不在第![]() 个正三角形边上的顶点
个正三角形边上的顶点![]() 的横坐标是
的横坐标是![]() ,则
,则![]() .
.
其中正确结论的序号是___________.(把你认为正确结论的序号都填上)
科目:高中数学 来源: 题型:
【题目】为调查中学生平均每人每天参加体育锻炼的时间![]() (单位:
(单位:![]() ),按锻炼时间分下列四种情况统计:(1)
),按锻炼时间分下列四种情况统计:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() 以上,有10000名中学生参加了此项活动,下图是此次调查中某一项的流程图,若平均每天参加体育锻炼的时间在
以上,有10000名中学生参加了此项活动,下图是此次调查中某一项的流程图,若平均每天参加体育锻炼的时间在![]() 的学生频率是0.15,则输出的结果为________.
的学生频率是0.15,则输出的结果为________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别是a,b,c,已知sinC+cosC=1-sin![]() .
.
(1)求sinC的值;
(2)若a2+b2=4(a+b)-8,求边c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某课程考核分理论与实验两部分进行,每部分考核成绩只记“合格”与“不合格”,两部分考核都是“合格”,则该课程考核“合格”,若甲、乙、丙三人在理论考核中合格的概率分别为0.9,0.8,0.7,在实验考核中合格的概率分别为0.8,0.7,0.9,所有考核是否合格相互之间没有影响.
(1)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
(2)求这三个人该课程考核都合格的概率(结果保留三位小数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某航运公司用300万元买回客船一艘,此船投入营运后,毎月需开支燃油费、维修费、员工工资,已知每月燃油费7000元,第![]() 个月的维修费和工资支出为
个月的维修费和工资支出为![]() 元.
元.
(1)设月平均消耗为![]() 元,求
元,求![]() 与
与![]() (月)的函数关系;
(月)的函数关系;
(2)投入营运第几个月,成本最低?(月平均消耗最小)
(3)若第一年纯收入50万元(已扣除消耗),以后每年纯收入以5%递减,则多少年后可收回成本?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两城市![]() 和
和![]() 相距
相距![]() ,现计划在两城市外以
,现计划在两城市外以![]() 为直径的半圆
为直径的半圆![]() 上选择一点
上选择一点![]() 建造垃圾处理场,其对城市的影响度与所选地点到城市的距离有关,对城
建造垃圾处理场,其对城市的影响度与所选地点到城市的距离有关,对城![]() 和城
和城![]() 的总影响度为城
的总影响度为城![]() 和城
和城![]() 的影响度之和,记
的影响度之和,记![]() 点到城
点到城![]() 的距离为
的距离为![]() ,建在
,建在![]() 处的垃圾处理场对城
处的垃圾处理场对城![]() 和城
和城![]() 的总影响度为
的总影响度为![]() ,统计调查表明:垃圾处理场对城
,统计调查表明:垃圾处理场对城![]() 的影响度与所选地点到城
的影响度与所选地点到城![]() 的距离的平方成反比,比例系数为4,对城
的距离的平方成反比,比例系数为4,对城![]() 的影响度与所选地点到城
的影响度与所选地点到城![]() 的距离的平方成反比,比例系数为
的距离的平方成反比,比例系数为![]() ,当垃圾处理场建在
,当垃圾处理场建在![]() 的中点时,对城
的中点时,对城![]() 和城
和城![]() 的总影响度为0.065;
的总影响度为0.065;
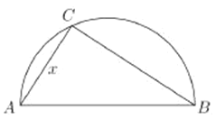
(1)将![]() 表示成
表示成![]() 的函数;
的函数;
(2)判断![]() 上是否存在一点,使建在此处的垃圾处理场对城
上是否存在一点,使建在此处的垃圾处理场对城![]() 和城
和城![]() 的总影响度最小?若存在,求出该点到城
的总影响度最小?若存在,求出该点到城![]() 的距离;若不存在,说明理由;
的距离;若不存在,说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点为平面直角坐标系
的顶点为平面直角坐标系![]() 的坐标原点
的坐标原点![]() ,焦点为圆
,焦点为圆![]() 的圆心
的圆心![]() .经过点
.经过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,交圆
两点,交圆![]() 于
于![]() 两点,
两点,![]() 在第一象限,
在第一象限,![]() 在第四象限.
在第四象限.
(1)求抛物线![]() 的方程;
的方程;
(2)是否存在直线![]() 使
使![]() 是
是![]() 与
与![]() 的等差中项?若存在,求直线
的等差中项?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某摩托车生产企业,上年度生产摩托车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销售量为1000辆.本年度为适应市场需求,计划提高产品档次,适度增加投入成本.若每辆车投入成本增加的比例为x(0<x<1),则出厂价相应的提高比例为0.75x,同时预计年销售量增加的比例为0.6x.已知年利润=(出厂价﹣投入成本)×年销售量.
(1)写出本年度预计的年利润y与投入成本增加的比例x的关系式;
(2)为使本年度的年利润比上年有所增加,问投入成本增加的比例x应在什么范围内?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com