练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数．

    （1）请在所给的平面直角坐标系中画出函数的图象；

    （2）根据函数的图象回答下列问题：①求函数的单调区间；

    ②求函数的值域；③求关于的方程在区间上解的个数．（回答上述3个小题都只需直接写出结果，不需给出演算步骤）

    【答案】（1）见解析；（2）①函数的单调递增区间为；函数的单调递减区间为；②函数的值域为；③方程在区间上解的个数为1个.

    【解析】

    （1）可先去绝对值变成分段函数后再画图，也可直接用画图的三步“列表，描点，连线”直接画图；（2）①图象向上去的部分对应的是增区间，向下来的部分对应的是减区间；②观察图象找出最低点和最高点即为函数的最小和最大值；③数形结合画图观察交点个数即可.

    （1）作图要规范：每条线上必须标明至少两个点的坐标，不在坐标轴上的点要用虚线标明对应的坐标值（教科书第28页例题的要求）（有一条直线没有标明点的坐标扣1分，两条都没标扣2分） ,

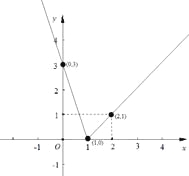
    （2）①函数的单调递增区间为；

    函数的单调递减区间为；

    ②函数的值域为；

    ③方程在区间上解的个数为1个 .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用年的隔热层，每厘米厚的隔热层建造成本为万元.该建筑物每年的能源消耗费用（单位：万元）与隔热层厚度（单位：厘米）满足关系：.若不建隔热层，每年的能源消耗费用为万元.设为隔热层建造费用与年的能源消耗费用之和.

    （1）求的值及的表达式；

    （2）隔热层修建多厚时，总费用最小，并求其最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】学校艺术节对同一类的，，，四项参赛作品，只评一项一等奖，在评奖揭晓前，甲、乙、丙、丁四位同学对这四项参赛作品预测如下：

    甲说：“是或作品获得一等奖”；

    乙说：“作品获得一等奖”；

    丙说：“，两项作品未获得一等奖”；

    丁说：“是作品获得一等奖”.

    若这四位同学中只有两位说的话是对的，则获得一等奖的作品是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】第届世界杯足球赛在俄罗斯进行，某校足球协会为了解该校学生对此次足球盛会的关注情况，随机调查了该校名学生，并将这名学生分为对世界杯足球赛“非常关注”与“一般关注”两类，已知这名学生中男生比女生多人，对世界杯足球赛“非常关注”的学生中男生人数与女生人数之比为，对世界杯足球赛“一般关注”的学生中男生比女生少人.

    （1）根据题意建立列联表，判断是否有的把握认为男生与女生对世界杯足球赛的关注有差异？

    （2）该校足球协会从对世界杯足球赛“非常关注”的学生中根据性别进行分层抽样，从中抽取人，再从这人中随机选出人参与世界杯足球赛宣传活动，求这人中至少有一个男生的概率.

    附：，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥中，，，为的中点．

    （1）证明：平面；

    （2）若点在棱上，且，求点到平面的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）若函数的图像与轴无交点，求的取值范围；

    （2）若方程在区间上存在实根，求的取值范围；

    （3）设函数，，当时若对任意的，总存在，使得，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．

    （1）求图中的值；

    （2）根据频率分布直方图，估计这100名学生语文成绩的平均分，众数，中位数；

    （3）若这100名学生语文成绩某些分数段的人数（）与数学成绩相应分数段的人数（）之比如下表所示，求数学成绩在[50，90）之外的人数．

    分数段

    [50，60）

    [60，70）

    [70，80）

    [80，90）

    1：1

    2：1

    3：4

    4：5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某种树苗栽种时高度为A(A为常数)米，栽种n年后的高度记为f(n)．经研究发现f(n)近似地满足 f(n)＝，其中，a，b为常数，n∈N，f(0)＝A．已知栽种3年后该树木的高度为栽种时高度的3倍．

    （1）栽种多少年后，该树木的高度是栽种时高度的8倍；

    （2）该树木在栽种后哪一年的增长高度最大．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a≥2,不等式logax+loga[(a+1)ak-1-x]≥2k-1的解集为A,其中a∈N*,k∈N.

    (1)求A.

    (2)设f(k)表示A中自然数个数,求和Sn=f(1)+f(2)+…+f(n).

    (3)当a=2时,比较Sn与n2+n的大小,并证明你的结论.

    查看答案和解析>>

    同步练习册答案