
【题目】已知抛物线![]() :
:![]() 上的点
上的点![]() 到其焦点
到其焦点![]() 的距离为
的距离为![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ) 已知直线![]() 不过点
不过点![]() 且与
且与![]() 相交于
相交于![]() ,
,![]() 两点,且直线
两点,且直线![]() 与直线
与直线![]() 的斜率之积为1,证明:
的斜率之积为1,证明:![]() 过定点.
过定点.
【答案】(Ⅰ)y2=x;(Ⅱ)证明见解析.
【解析】试题分析:![]() 由题意求得
由题意求得![]() ,再根据抛物线的定义推导出
,再根据抛物线的定义推导出![]() ,求得
,求得![]() 的值,代入即可求得
的值,代入即可求得![]() 的方程
的方程![]() 证法一:设直线
证法一:设直线![]() 的方程为
的方程为![]() ,联立方程解出
,联立方程解出![]() ,
,![]() 代入求出结果;证法二:设
代入求出结果;证法二:设![]()
表示出![]() ,设
,设![]() :
:![]() ,联立直线与抛物线方程得
,联立直线与抛物线方程得![]() ,
,![]() ,代入
,代入![]() 求出结果;证法三:设
求出结果;证法三:设![]() :
:![]() ,联立直线与抛物线方程,代入
,联立直线与抛物线方程,代入![]() ,化简求出结果
,化简求出结果
解析:(Ⅰ)由题意,得![]() ,即
,即![]() .
.
由抛物线的定义,得![]() .
.
由题意,![]() .解得
.解得![]() ,或
,或![]() (舍去).
(舍去).
所以![]() 的方程为
的方程为![]() .
.
(Ⅱ)证法一:设直线![]() 的斜率为
的斜率为![]() (显然
(显然![]() ),则直线
),则直线![]() 的方程为
的方程为![]() ,则
,则![]() .
.
由![]() 消去
消去![]() 并整理得
并整理得![]()
![]() .
.
设![]() ,由韦达定理,得
,由韦达定理,得![]() ,即
,即![]() .
.
![]()
![]() .所以
.所以![]() .
.
由题意,直线![]() 的斜率为
的斜率为![]() .
.
同理可得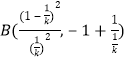 ,即
,即![]() .
.
若直线![]() 的斜率不存在,则
的斜率不存在,则![]() .解得
.解得![]() ,或
,或![]() .
.
当![]() 时,直线
时,直线![]() 与直线
与直线![]() 的斜率均为
的斜率均为![]() ,
,![]() ,
,![]() 两点重合,与题意不符;
两点重合,与题意不符;
当![]() 时,直线
时,直线![]() 与直线
与直线![]() 的斜率均为
的斜率均为![]() ,
,![]() ,
,![]() 两点重合,与题意不符.
两点重合,与题意不符.
所以,直线![]() 的斜率必存在.
的斜率必存在.
直线![]() 的方程为
的方程为![]()
![]() ,即
,即![]() .
.
所以直线![]() 过定点
过定点![]() .
.
证法二:由(1),得![]() .
.
若![]() 的斜率不存在,则
的斜率不存在,则![]() 与
与![]() 轴垂直.
轴垂直.
设![]() ,则
,则![]() ,
,![]() .
.
则![]()
![]()
![]() .
.
(![]() ,否则,
,否则,![]() ,则
,则![]() ,或
,或![]() ,直线
,直线![]() 过点
过点![]() ,与题设条件矛盾)
,与题设条件矛盾)
由题意,![]() ,所以
,所以![]() .这时
.这时![]() ,
,![]() 两点重合,与题意不符.
两点重合,与题意不符.
所以![]() 的斜率必存在.
的斜率必存在.
设![]() 的斜率为
的斜率为![]() ,显然
,显然![]() ,设
,设![]() :
:![]() ,
,
由直线![]() 不过点
不过点![]() ,所以
,所以![]() .
.
由![]() 消去
消去![]() 并整理得
并整理得![]() .
.
由判别式![]() ,得
,得![]() .
.
设![]() ,
,![]() ,则
,则![]() ①,
①,![]() ②,
②,
则![]()
![]()
![]() .
.
由题意,![]() .
.
故![]()
![]() ③
③
将①②代入③式并化简整理得![]() ,即
,即![]() .
.
即![]() ,即
,即![]() .
.
又![]() ,即
,即![]() ,所以
,所以![]() ,即
,即![]() .
.
所以![]() :
:![]() .显然
.显然![]() 过定点
过定点![]() .
.
证法三:由(1),得![]() .
.
设![]() :
:![]() ,由直线
,由直线![]() 不过点
不过点![]() ,所以
,所以![]() .
.
由![]() 消去
消去![]() 并整理得
并整理得![]() .
.
由题意,判别式![]() .
.
设![]() ,
,![]() ,则
,则![]() ①,
①,![]() ②
②
则![]()
![]()
![]() .
.
由题意,![]() ,即
,即![]() ③
③
将①②代入③式得![]() ,即
,即![]() .
.
所以![]() :
:![]() .显然
.显然![]() 过定点
过定点![]() .
.


科目:高中数学 来源: 题型:
【题目】某市大力推广纯电动汽车,对购买用户依照车辆出厂续驶里程![]() 的行业标准,予以地方财政补贴.其补贴标准如下表:
的行业标准,予以地方财政补贴.其补贴标准如下表:

2017年底随机调査该市1000辆纯电动汽车,统计其出厂续驶里程![]() ,得到频率分布直方图如图所示.
,得到频率分布直方图如图所示.
用样本估计总体,频率估计概率,解决如下问题:
(1)求该市纯电动汽车2017年地方财政补贴的均值;
(2)某企业统计2017年其充电站100天中各天充电车辆数,得如下的频数分布表:

(同一组数据用该区间的中点值作代表)
2018年2月,国家出台政策,将纯电动汽车财政补贴逐步转移到充电基础设施建设上来.该企业拟将转移补贴资金用于添置新型充电设备.现有直流、交流两种充电桩可供购置.直流充电桩5万元/台,每台每天最多可以充电30辆车,每天维护费用500元/台; 交流充电桩1万元/台,每台每天最多可以充电4辆车,每天维护费用80元/台.
该企业现有两种购置方案:
方案一:购买100台直流充电桩和900台交流充电桩;
方案二:购买200台直流充电桩和400台交流充电桩.
假设车辆充电时优先使用新设备,且充电一辆车产生25元的收入,用2017年的统计数据,分别估计该企业在两种方案下新设备产生的日利润.(日利润![]() 日收入
日收入![]() 日维护费用)
日维护费用)
查看答案和解析>>
科目:高中数学 来源: 题型:
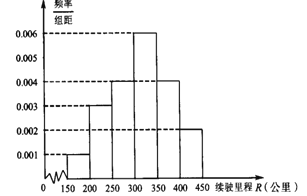
【题目】某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:
(Ⅰ)依据频率分布直方图估算该运动员投篮命中时,他到篮筐中心的水平距离的中位数;
(Ⅱ)在某场比赛中,考察他前4次投篮命中到篮筐中心的水平距离的情况,并且规定:运动员投篮命中时,他到篮筐中心的水平距离不少于4米的记1分,否则扣掉1分.用随机变量X表示第4次投篮后的总分,将频率视为概率,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 截以坐标原点
截以坐标原点![]() 为圆心的圆所得的弦长为
为圆心的圆所得的弦长为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 切于第一象限,且与坐标轴交于点
切于第一象限,且与坐标轴交于点![]() ,
,![]() ,当
,当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)设![]() ,
,![]() 是圆
是圆![]() 上任意两点,点
上任意两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,若直线
,若直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() 和
和![]() ,问
,问![]() 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:
(Ⅰ)依据频率分布直方图估算该运动员投篮命中时,他到篮筐中心的水平距离的中位数;
(Ⅱ)在某场比赛中,考察他前4次投篮命中到篮筐中心的水平距离的情况,并且规定:运动员投篮命中时,他到篮筐中心的水平距离不少于4米的记1分,否则扣掉1分.用随机变量X表示第4次投篮后的总分,将频率视为概率,求X的分布列和数学期望.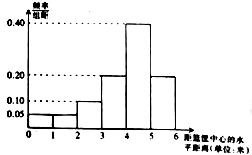
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某名校从2008年到2017年考入清华、北大的人数可以通过以下表格反映出来.(为了方便计算,将2008年编号为1,2009年编号为2,以此类推……)
年份 |
|
|
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
|
(1)根据最近5年的数据,利用最小二乘法求出![]() 与
与![]() 之间的线性回归方程,并用以预测2018年该校考入清华、北大的人数;(结果要求四舍五入至个位)
之间的线性回归方程,并用以预测2018年该校考入清华、北大的人数;(结果要求四舍五入至个位)
(2)从这10年的数据中随机抽取2年,记其中考入清华、北大的人数不少于![]() 的有
的有![]() 年,
年,
求![]() 的分布数列和数学期望.
的分布数列和数学期望.
参考公式: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2019迎新年联欢会上,为了活跃大家气氛,设置了“摸球中奖”游戏,桌子上放置一个不透明的箱子,箱子中有3个黄色、3个白色的乒乓球(其体积、质地完全相同)游戏规则:从箱子中随机摸出3个球,若摸得同一颜色的3个球,摸球者中奖价值50元奖品;若摸得非同一颜色的3个球,摸球者中奖价值20元奖品.
(1)摸出的3个球为白球的概率是多少?
(2)假定有10人次参与游戏,试从概率的角度估算一下需要准备多少元钱购买奖品?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小区抽取100户居民进行月用电量调查,发现其用电量都在50度至350度之间,频率分布直方图如图所示. 
(1)根据直方图求x的值,并估计该小区100户居民的月均用电量(同一组中的数据用该组区间的中点值作代表);
(2)从该小区已抽取的100户居民中,随机抽取月用电量超过250度的3户,参加节约用电知识普及讲座,其中恰有ξ户月用电量超过300度,求ξ的分布列及期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com