
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处切线与直线
处切线与直线![]() 垂直.
垂直.
(1)试比较![]() 与
与![]() 的大小,并说明理由;
的大小,并说明理由;
(2)若函数![]() 有两个不同的零点
有两个不同的零点![]() ,
,![]() ,证明:
,证明:![]() .
.
科目:高中数学 来源: 题型:
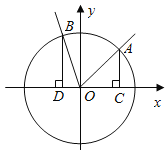
【题目】(本小题满分13分)如图,在直角坐标系![]() 中,角
中,角![]() 的顶点是原点,始边与
的顶点是原点,始边与![]() 轴正半轴重合.终边交单位圆于点
轴正半轴重合.终边交单位圆于点![]() ,且
,且![]() ,将角
,将角![]() 的终边按逆时针方向旋转
的终边按逆时针方向旋转![]() ,交单位圆于点
,交单位圆于点![]() ,记
,记![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)分别过![]() 作
作![]() 轴的垂线,垂足依次为
轴的垂线,垂足依次为![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,若
,若![]() ,求角
,求角![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足①对于任意
满足①对于任意![]() ,都有
,都有![]() ;②
;②![]() ;③
;③![]() 的图像与
的图像与![]() 轴的两个交点之间的距离为4.
轴的两个交点之间的距离为4.
(1)求![]() 的解析式;
的解析式;
(2)记![]()
①若![]() 为单调函数,求
为单调函数,求![]() 的取值范围;
的取值范围;
②记![]() 的最小值为
的最小值为![]() ,讨论函数
,讨论函数![]() 零点的个数.
零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若存在距离为
,若存在距离为![]() 的两条直线
的两条直线![]() 和
和![]() ,使得对任意
,使得对任意![]() 都有
都有![]() 恒成立,则称函数
恒成立,则称函数![]() 有一个宽度为
有一个宽度为![]() 的通道.给出下列函数:
的通道.给出下列函数:
①![]() ; ②
; ②![]() ; ③
; ③![]() ; ④
; ④![]() .
.
其中在区间![]() 上有一个通道宽度为
上有一个通道宽度为![]() 的函数是__________(写出所有正确的序号).
的函数是__________(写出所有正确的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间生产某种电子元件,如果生产出一件正品,可获利200元,如果生产出一件次品,则损失100元.已知该车间制造电子元件的过程中,次品率![]() 与日产量
与日产量![]() 的函数关系是:
的函数关系是:![]() .
.
(1)写出该车间的日盈利额![]() (元)与日产量
(元)与日产量![]() (件)之间的函数关系式;
(件)之间的函数关系式;
(2)为使日盈利额最大,该车间的日产量应定为多少件?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】华为手机作为华为公司三大核心业务之一,2018年的销售量跃居全球第二名,某机构随机选取了100名华为手机的顾客进行调查,并将这![]() 人的手机价格按照
人的手机价格按照![]() ,
,![]() ,…
,…![]() 分成
分成![]() 组,制成如图所示的频率分布直方图,其中
组,制成如图所示的频率分布直方图,其中![]() 是
是![]() 的
的![]() 倍.
倍.

(1)求![]() ,
,![]() 的值;
的值;
(2)求这![]() 名顾客手机价格的平均数(同一组中的数据用该组区间的中间值作代表);
名顾客手机价格的平均数(同一组中的数据用该组区间的中间值作代表);
(3)利用分层抽样的方式从手机价格在![]() 和
和![]() 的顾客中选取
的顾客中选取![]() 人,并从这
人,并从这![]() 人中随机抽取
人中随机抽取![]() 人进行回访,求抽取的
人进行回访,求抽取的![]() 人手机价格在不同区间的概率.
人手机价格在不同区间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com