
【题目】如图,三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() .以
.以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,连接
,连接![]() 和
和![]() .
.
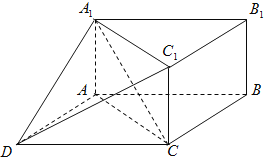
(1)求证:![]() 平面
平面![]() ;
;
(2)若二面角![]() 为45°,
为45°,
①证明:平面![]() 平面
平面![]() ;
;
②求直线![]() 与平面
与平面![]() 所成角的正切值.
所成角的正切值.
【答案】(1)详见解析;(2)①详见解析;②![]() .
.
【解析】
(1)连接![]() ,证明
,证明![]() ,再利用线面平行的判定定理证明.
,再利用线面平行的判定定理证明.
(2)①取CD的中点O,连接![]() ,易证
,易证![]() 为二面角
为二面角![]() 的平面角,得到
的平面角,得到![]() ,结合
,结合![]() 平面
平面![]() ,得到
,得到![]() ,从而得到
,从而得到![]() 平面
平面![]() ,再利用
,再利用![]() ,由面面垂直的判定定理证明,②过A作
,由面面垂直的判定定理证明,②过A作![]() ,根据平面
,根据平面![]() 平面
平面![]() ,得到
,得到![]() 平面
平面![]() ,可知
,可知![]() 是直线
是直线![]() 与平面
与平面![]() 所成角,然后在
所成角,然后在![]() 中求解.
中求解.
(1)如图所示
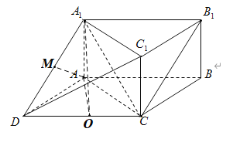
连接![]() ,在平行四边形ABCD中,
,在平行四边形ABCD中,![]() ,
,
在三棱柱![]() 中,又
中,又![]() ,
,
所以![]() ,
,
所以四边形![]() 是平行四边形,
是平行四边形,
所以![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(2)①取CD的中点O,连接![]() ,因为
,因为![]() ,
,
所以![]() ,又因为
,又因为![]() 平面
平面![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() ,
,
所以![]() 为二面角
为二面角![]() 的平面角,
的平面角,
在![]() 中,
中,![]() ,
,![]() ,
,
所以![]() ,又因为
,又因为![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ;
;
②过A作![]() ,因为平面
,因为平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() 是
是![]() 在平面
在平面![]() 上的射影,
上的射影,
所以![]() 是直线
是直线![]() 与平面
与平面![]() 所成角,
所成角,
在![]() 中,
中,![]() ,
,
![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在2019年高考数学的全国Ⅲ卷中,文科和理科的选做题题目完全相同,第22题考查选修4-4:极坐标和参数方程;第23题考查选修4-5:不等式选讲.某校高三质量检测的命题采用了全国Ⅲ卷的形式,在测试结束后,该校数学组教师对该校全体高三学生的选做题得分情况进行了统计,得到两题得分的![]() 列联表如下(已知每名学生只做了一道题):
列联表如下(已知每名学生只做了一道题):
选做22题 | 选做23题 | 合计 | |
文科人数 | 50 | 60 | |
理科人数 | 40 | ||
总计 | 400 |
(1)完善![]() 列联表中的数据,判断能否有
列联表中的数据,判断能否有![]() 的把握认为“选做题的选择”与“文、理科的科类”有关;
的把握认为“选做题的选择”与“文、理科的科类”有关;
(2)经统计,第23题得分为0的学生中,理科生占理科总人数的![]() ,文科生占文科总人数的
,文科生占文科总人数的![]() ,在按分层抽样的方法在第23题得分为0的学生中随机抽取6名进行单独辅导,并在辅导后随机抽取2名学生进行测试,求被抽中进行测试的2名学生均为理科生的概率.
,在按分层抽样的方法在第23题得分为0的学生中随机抽取6名进行单独辅导,并在辅导后随机抽取2名学生进行测试,求被抽中进行测试的2名学生均为理科生的概率.
附: ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() ,
,![]() 的值;
的值;
(2)若函数![]() 在
在![]() 和
和![]() 两处取得极值,求实数
两处取得极值,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2010年至2018年之间,受益于基础设施建设对光纤产品的需求,以及个人计算机及智能手机的下一代规格升级,电动汽车及物联网等新机遇,全球连接器行业增长呈现加速状态.根据如下折线图,下列结论正确的个数为( )
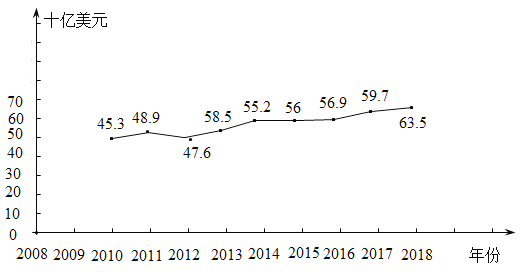
①每年市场规模逐年增加;
②市场规模增长最快的是2013年至2014年;
③这8年的市场规模增长率约为40%;
④2014年至2018年每年的市场规模相对于2010年至2014年每年的市场规模,数据方差更小,变化比较平稳.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示在菱形ABCD中,![]() ,
,![]() ,点E是AD的中点,将
,点E是AD的中点,将![]() 沿BE折起,使得平面
沿BE折起,使得平面![]() 平面BCDE得到如图2所示的四棱锥
平面BCDE得到如图2所示的四棱锥![]() ,点F为AC的中点.在图2中
,点F为AC的中点.在图2中
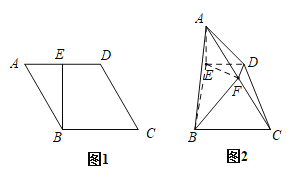
(Ⅰ)证明:![]() 平面ABE;
平面ABE;
(Ⅱ)求点A到平面BEF的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,
时,
①若曲线![]() 与直线
与直线![]() 相切,求c的值;
相切,求c的值;
②若曲线![]() 与直线
与直线![]() 有公共点,求c的取值范围.
有公共点,求c的取值范围.
(2)当![]() 时,不等式
时,不等式![]() 对于任意正实数x恒成立,当c取得最大值时,求a,b的值.
对于任意正实数x恒成立,当c取得最大值时,求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关……”其大意为:“某人从距离关口三百七十八里处出发,第一天走得轻快有力,从第二天起,由于脚痛,每天走的路程为前一天的一半,共走了六天到达关口……” 那么该人第一天走的路程为______________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥P-ABC的平面展开图中,四边形ABCD为边长等于![]() 的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中:
的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中:

(1)证明:平面PAC⊥平面ABC;
(2)若点M为棱PA上一点且![]() ,求二面角P-BC-M的余弦值.
,求二面角P-BC-M的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线C的参数方程为:
中,曲线C的参数方程为: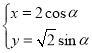 (
(![]() 为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为
为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为![]() .
.
(Ⅰ)求曲线C的普通方程和直线l的直角坐标方程;
(Ⅱ)设点P的直角坐标为![]() ,若直线l与曲线C分别相交于A,B两点,求
,若直线l与曲线C分别相交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com