
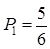 .(2)
.(2)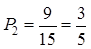 。(3)P
。(3)P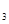 =
=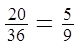
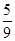
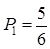 .
.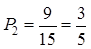 。
。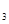 =
=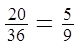


科目:高中数学 来源:不详 题型:单选题
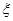 表示这5人中“三好学生”的人数,则下列概率中等于
表示这5人中“三好学生”的人数,则下列概率中等于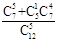 的是( )
的是( )A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,假设
,假设 互不相等,且假定各人能否完成任务的事件相互独立.
互不相等,且假定各人能否完成任务的事件相互独立. ,其中
,其中 是
是 的一个排列,求所需派出人员数目
的一个排列,求所需派出人员数目 的分布列和均值(数字期望)
的分布列和均值(数字期望) ;
; ,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com