
【题目】将函数f(x)=sinωx(ω>0)的图象向右平移 ![]() 个单位后得到函数g(x)的图象,若对于满足|f(x1)﹣g(x2)|=2的x1 , x2 , 有|x1﹣x2|min=
个单位后得到函数g(x)的图象,若对于满足|f(x1)﹣g(x2)|=2的x1 , x2 , 有|x1﹣x2|min= ![]() ,则f(
,则f( ![]() )的值为 .
)的值为 .
【答案】1
【解析】解:将函数f(x)=sinωx(ω>0)的图象向右平移 ![]() 个单位后得到函数g(x)=sinω(x﹣
个单位后得到函数g(x)=sinω(x﹣ ![]() )的图象,
)的图象,
若对于满足|f(x1)﹣g(x2)|=2的x1,x2,有|x1﹣x2|min= ![]() ,则
,则 ![]() ﹣
﹣ ![]() =
= ![]() ,∴T=
,∴T= ![]() =π,∴ω=2,
=π,∴ω=2,
f(x)=sin2x,
则f( ![]() )=sin
)=sin ![]() =1,
=1,
所以答案是:1.
【考点精析】本题主要考查了函数y=Asin(ωx+φ)的图象变换的相关知识点,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能正确解答此题.
的图象才能正确解答此题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】在区间D上,如果函数f(x)为减函数,而xf(x)为增函数,则称f(x)为D上的弱减函数.若f(x)= ![]()
(1)判断f(x)在区间[0,+∞)上是否为弱减函数;
(2)当x∈[1,3]时,不等式 ![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若函数g(x)=f(x)+k|x|﹣1在[0,3]上有两个不同的零点,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系内,已知A(3,3)是⊙C上一点,折叠该圆两次使点A分别与圆上不相同的两点(异于点A)重合,两次的折痕方程分别为x﹣y+1=0和x+y﹣7=0,若⊙C上存在点P,使∠MPN=90°,其中M、N的坐标分别为(﹣m,0)(m,0),则m的最大值为( )
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产甲、乙两种产品所得利润分别为P和Q(万元),它们与投入资金m(万元)的关系有经验公式P= ![]() m+65,Q=76+4
m+65,Q=76+4 ![]() ,今将150万元资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投资金额不低于25万元.
,今将150万元资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投资金额不低于25万元.
(1)设对乙产品投入资金x万元,求总利润y(万元)关于x的函数关系式及其定义域;
(2)如何分配使用资金,才能使所得总利润最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,AA1=12,
点D是AB的中点.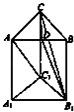
(1)求证:AC⊥B1C
(2)求证:AC1∥平面CDB1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(﹣2,2).
=(﹣2,2).
(1)若 ![]() =
= ![]() ,求(sinα+cosα)2的值;
,求(sinα+cosα)2的值;
(2)若 ![]() ,求sin(π﹣α)sin(
,求sin(π﹣α)sin( ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+4x+a﹣5,g(x)=m4x﹣1﹣2m+7.
(1)若函数f(x)在区间[﹣1,1]上存在零点,求实数a的取值范围;
(2)当a=0时,若对任意的x1∈[1,2],总存在x2∈[1,2],使f(x1)=g(x2)成立,求实数m的取值范围;
(3)若y=f(x)(x∈[t,2])的置于为区间D,是否存在常数t,使区间D的长度为6﹣4t?若存在,求出t的值;若不存在,请说明理由. (注:区间[p,q]的长度q﹣p)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆的中心在原点O,短轴长为 ![]() ,左焦点为F(﹣c,0)(c>0),直线
,左焦点为F(﹣c,0)(c>0),直线 ![]() 与x轴交于点A,且
与x轴交于点A,且 ![]() ,过点A的直线与椭圆相交于P,Q两点.
,过点A的直线与椭圆相交于P,Q两点. 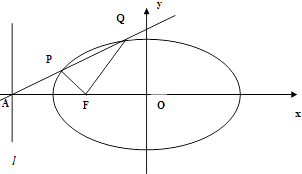
(1)求椭圆的方程.
(2)若 ![]() ,求直线PQ的方程.
,求直线PQ的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com