
【题目】已知函数f(x)=![]() ,若数列{an}(n∈N*)满足:a1=1,an+1=f(an).
,若数列{an}(n∈N*)满足:a1=1,an+1=f(an).
(1)证明数列{![]() }为等差数列,并求数列{an}的通项公式.
}为等差数列,并求数列{an}的通项公式.
(2)设数列{cn}满足:cn=![]() ,求数列{cn}的前n项的和Sn.
,求数列{cn}的前n项的和Sn.
【答案】(1) 见解析(2) Sn=(n-1)2n+1+2.
【解析】试题分析:(1)先根据函数解析式得数列递推关系,再取倒数得到{![]() }递推关系,根据等差数列定义可判断为等差数列,根据等差数列通项公式求得
}递推关系,根据等差数列定义可判断为等差数列,根据等差数列通项公式求得![]() ,再取倒数得数列{an}的通项公式.(2)根据错位相减法求数列{cn}的前n项的和,注意相减时符号变化,求和时项数得确定,最后不要忘记除以1-q
,再取倒数得数列{an}的通项公式.(2)根据错位相减法求数列{cn}的前n项的和,注意相减时符号变化,求和时项数得确定,最后不要忘记除以1-q
试题解析:(1)因为f(x)=![]() ,所以an+1=f(an)=
,所以an+1=f(an)=![]() ,
,
所以![]() -
-![]() =1,{
=1,{![]() }是等差数列,
}是等差数列,
an=![]() .
.
(2)cn=n·2n,
所以Sn=1×2+2×22+…+n·2n,
2Sn=1×22+2×23+…+(n-1)2n+n·2n+1,
所以2Sn-Sn=Sn=-2-22-23…-2n+n·2n+1
= (n-1)2n+1+2.
所以Sn=(n-1)2n+1+2.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:高中数学 来源: 题型:
【题目】自2016年下半年起六安市区商品房价不断上涨,为了调查研究六安城区居民对六安商品房价格承受情况,寒假期间小明在六安市区不同小区分别对50户居民家庭进行了抽查,并统计出这50户家庭对商品房的承受价格(单位:元/平方),将收集的数据分成![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五组(单位:元/平方),并作出频率分布直方图如图:
五组(单位:元/平方),并作出频率分布直方图如图:
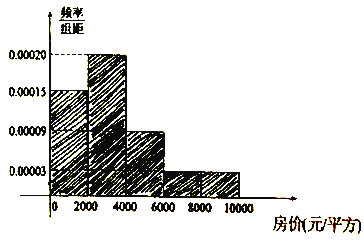
(Ⅰ)试根据频率分布直方图估计出这50户家庭对商品房的承受价格平均值(单位:元/平方);
(Ⅱ)为了作进一步调查研究,小明准备从承受能力超过4000元/平方的居民中随机抽出2户进行再调查,设抽出承受能力超过8000元/平方的居民为![]() 户,求
户,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中, ![]() ,
, ![]() .
. ![]() ,且
,且![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 为
为![]() 上任意一点.
上任意一点.
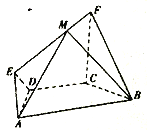
(1)求证: ![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动(包括两端点),若平面
上运动(包括两端点),若平面![]() 与平面
与平面![]() 所成的锐二面角为60°,试确定点
所成的锐二面角为60°,试确定点![]() 的位置.
的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,a,b,c分别是△ABC三个内角A,B,C的对边,下列四个命题:
①若tanA+tanB+tanC>0,则△ABC是锐角三角形
②若acoA=bcosB,则△ABC是等腰三角形
③若bcosC+ccosB=b,则△ABC是等腰三角形
④若 ![]() =
= ![]() ,则△ABC是等边三角形
,则△ABC是等边三角形
其中正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 关于直线
关于直线![]() 对称,圆心
对称,圆心![]() 在第二象限,半径为
在第二象限,半径为![]() .
.
(Ⅰ)求圆![]() 的方程.
的方程.
(Ⅱ)是否存在直线![]() 与圆
与圆![]() 相切,且在
相切,且在![]() 轴、
轴、![]() 轴上的截距相等?若存在,写出满足条件的直线条数(不要求过程);若不存在,说明理由.
轴上的截距相等?若存在,写出满足条件的直线条数(不要求过程);若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,a,b,c分别是角A,B,C的对边,且a=80,b=100,A= ![]() ,则此三角形是( )
,则此三角形是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.锐角或钝角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,
,![]() ,
,![]() 为
为![]() 中点.
中点.
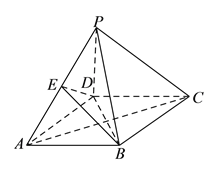
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 的交点记为
的交点记为![]() ,求证
,求证![]() 平面
平面![]() ;
;
(3)在(2)的条件下求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com