
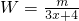 ,(0≤x≤15),若不建隔热层,每年能耗为10万元.设f(x)为隔热层的建造费用与30年总计的能耗费用之和.
,(0≤x≤15),若不建隔热层,每年能耗为10万元.设f(x)为隔热层的建造费用与30年总计的能耗费用之和.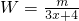 ,(0≤x≤15),
,(0≤x≤15), =10,
=10,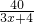 ,(0≤x≤15).
,(0≤x≤15).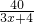 +6x=
+6x= +6x(0≤x≤15).
+6x(0≤x≤15). =99.
=99.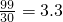 (万元),
(万元),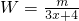 ,(0≤x≤15),若不建隔热层,每年能源消耗费用为10万元.我们可得W(0)=10,解得m=40.故W=
,(0≤x≤15),若不建隔热层,每年能源消耗费用为10万元.我们可得W(0)=10,解得m=40.故W=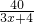 ,(0≤x≤15).根据隔热层建造费用与30年的能源消耗费用之和为f(x),我们不难得到f(x)的表达式.
,(0≤x≤15).根据隔热层建造费用与30年的能源消耗费用之和为f(x),我们不难得到f(x)的表达式. =99.故x=4时,以隔热层使用寿命30年计算,平均每年需
=99.故x=4时,以隔热层使用寿命30年计算,平均每年需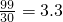 (万元),由此能求出以隔热层使用寿命30年计算,平均每年比不建隔热层节约钱数.
(万元),由此能求出以隔热层使用寿命30年计算,平均每年比不建隔热层节约钱数.

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
| k | 3x+5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| k | 3x+5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| k |
| 3x+5 |
| a |
| x |
| a |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
| k | 2x+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m | 3x+4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com