
°æƒø°ø∫”ƒœ∂‡µÿ‘‚”ˆøÁƒÍˆ≤£¨∫‹∂‡—ß–£µ˜’˚‘™µ©∑≈ºŸ ±º‰£¨Ã·«∞∑≈ºŸ»√—ß…˙√«‘⁄º“¿Ô∂„ˆ≤£¨÷£÷› –∏˘æ›°∂÷£÷› –»À√Ò’˛∏Æ∞Ïπ´Ã¸πÿ”⁄Ω´÷ÿŒ€»æÃÏ∆¯ª∆…´‘§æØ…˝º∂Œ™∫Ï…´‘§æصƒÕ®÷™°∑.◊‘12‘¬29»’12 ±Ω´ª∆…´‘§æØ…˝º∂Œ™∫Ï…´‘§æØ£¨12‘¬30»’0 ±∆Ù∂ØIº∂œÏ”¶£¨√˜»∑“™«Û£∫°∞”◊∂˘‘∞°¢÷––°—ßµ»ΩÔ˝ª˙ππÕ£øŒ£¨Õ£øŒ≤ªÕ£—ß°±£¨—ß…˙∫Õº“≥§∂‘Õ£øŒ’‚“ªæŸ¥Î∞˝±·≤ª“ª£¨”–Œ™¡ÀΩ°øµ‘fi≥…µƒ£¨”–≈¬µ¢ŒÛ—ßœ∞≤ª‘fi≥…µƒ.ƒ≥µ˜≤Ȫ˙ππŒ™¡À¡ÀΩ‚π´÷⁄∂‘∏√查εƒÃ¨∂»£¨Àʪ˙µ˜≤È≤…∑√¡À50»À£¨Ω´µ˜≤È«Èøˆ’˚¿Ìª„◊‹≥…œ¬±Ì£∫
ƒÍ¡‰£®ÀÍ£© |
|
|
|
|
|
|
∆µ ˝ | 5 | 10 | 15 | 10 | 5 | 5 |
‘fi≥…»À ˝ | 4 | 6 | 9 | 6 | 3 | 4 |
£®1£©«Î≤π»´±ªµ˜≤È»À‘±ƒÍ¡‰µƒ∆µ¬ ∑÷≤º÷±∑ΩÕº£ª
£®2£©»Ù¥”ƒÍ¡‰‘⁄![]() µƒ±ªµ˜≤È’fl÷–∑÷±Àʪ˙—°»°“ª»ÀΩ¯––◊∑◊Ÿµ˜≤È£¨«Û’‚¡Ω»À∂º‘fi≥…°∞Õ£øŒ°±’‚“ªæŸ¥Îµƒ∏≈¬ .
µƒ±ªµ˜≤È’fl÷–∑÷±Àʪ˙—°»°“ª»ÀΩ¯––◊∑◊Ÿµ˜≤È£¨«Û’‚¡Ω»À∂º‘fi≥…°∞Õ£øŒ°±’‚“ªæŸ¥Îµƒ∏≈¬ .
°æ¥∞∏°ø£®1£©º˚Ω‚Œˆ£®2£©![]()
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ: (1)”…“—÷™ƒÍ¡‰‘⁄![]() ƒ⁄µƒ∆µ ˝Œ™15,∆µ¬ Œ™
ƒ⁄µƒ∆µ ˝Œ™15,∆µ¬ Œ™![]() ,π ‘⁄∆µ¬ ∑÷≤º÷±∑ΩÕº÷–µƒ∏flŒ™
,π ‘⁄∆µ¬ ∑÷≤º÷±∑ΩÕº÷–µƒ∏flŒ™![]() ,≤π»´÷±∑ΩÕº; (2)”…“—÷™Õº±Ì∑÷±’“≥ˆ¡Ω∏ˆƒÍ¡‰∂Œµƒ±ªµ˜≤È»À ˝∫Õ‘fi≥…°∞Õ£øŒ°±’‚“ªæŸ¥Îµƒ»À ˝,≤…”√¡–æŸ∑®«Û≥ˆ≥È»°µƒ¡Ω»À∂º‘fi≥…°∞Õ£øŒ°±’‚“ªæŸ¥Îµƒ∑Ω∑® ˝,”√π≈µ‰∏≈–Õ«Û≥ˆ≥È»°µƒ¡Ω»À∂º‘fi≥…°∞Õ£øŒ°±’‚“ªæŸ¥Îµƒ∏≈¬ .
,≤π»´÷±∑ΩÕº; (2)”…“—÷™Õº±Ì∑÷±’“≥ˆ¡Ω∏ˆƒÍ¡‰∂Œµƒ±ªµ˜≤È»À ˝∫Õ‘fi≥…°∞Õ£øŒ°±’‚“ªæŸ¥Îµƒ»À ˝,≤…”√¡–æŸ∑®«Û≥ˆ≥È»°µƒ¡Ω»À∂º‘fi≥…°∞Õ£øŒ°±’‚“ªæŸ¥Îµƒ∑Ω∑® ˝,”√π≈µ‰∏≈–Õ«Û≥ˆ≥È»°µƒ¡Ω»À∂º‘fi≥…°∞Õ£øŒ°±’‚“ªæŸ¥Îµƒ∏≈¬ .
‘Ã‚Ω‚Œˆ:£®1£©≤π»´∆µ¬ ∑÷≤º÷±∑ΩÕº»Áœ¬ÕºÀ˘ æ£∫
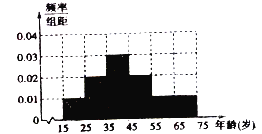
£®2£©ƒÍ¡‰‘⁄![]() µƒ±ªµ˜≤È’fl∑÷±”–5»À£¨5»À,∆‰÷–‘fi≥…°∞Õ£øŒ°±’‚“ªæŸ¥Îµƒ∑÷±”–3»À∫Õ4»À£¨¥”÷–∑÷±≥È»°1»Àµƒ∑Ω∑® ˝π≤”–25÷÷£¨
µƒ±ªµ˜≤È’fl∑÷±”–5»À£¨5»À,∆‰÷–‘fi≥…°∞Õ£øŒ°±’‚“ªæŸ¥Îµƒ∑÷±”–3»À∫Õ4»À£¨¥”÷–∑÷±≥È»°1»Àµƒ∑Ω∑® ˝π≤”–25÷÷£¨
…Ë![]() ±Ì æƒÍ¡‰‘⁄
±Ì æƒÍ¡‰‘⁄![]() µƒ±ªµ˜≤È’fl÷–‘fi≥…°∞Õ£øŒ°±’‚“ªæŸ¥Îµƒ3»À£¨
µƒ±ªµ˜≤È’fl÷–‘fi≥…°∞Õ£øŒ°±’‚“ªæŸ¥Îµƒ3»À£¨
![]() ±Ì æƒÍ¡‰‘⁄
±Ì æƒÍ¡‰‘⁄![]() µƒ±ªµ˜≤È’fl÷–‘fi≥…°∞Õ£øŒ°±’‚“ªæŸ¥Îµƒ4»À£¨
µƒ±ªµ˜≤È’fl÷–‘fi≥…°∞Õ£øŒ°±’‚“ªæŸ¥Îµƒ4»À£¨
ƒ«√¥≥È»°µƒ¡Ω»À∂º‘fi≥…°∞Õ£øŒ°±’‚“ªæŸ¥ÎµƒŒ™![]() π≤12÷÷.
π≤12÷÷.
π ≥È»°¡Ω»À∂º‘fi≥…°∞Õ£øŒ°±’‚“ªæŸ¥Îµƒ∏≈¬ Œ™![]() .
.


 ∆⁄ƒ©Ω≈∆æÌœµ¡–¥∞∏
∆⁄ƒ©Ω≈∆æÌœµ¡–¥∞∏ «·À…øŒÃ√±Í◊º¡∑œµ¡–¥∞∏
«·À…øŒÃ√±Í◊º¡∑œµ¡–¥∞∏
| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() £Æ
£Æ
£®1£©»Ù![]() ‘⁄«¯º‰
‘⁄«¯º‰![]() …œµ•µ˜µ›‘ˆ£¨«Û µ ˝
…œµ•µ˜µ›‘ˆ£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß£ª
µƒ»°÷µ∑∂Œß£ª
£®2£©»Ù¥Ê‘⁄Œ®“ª’˚ ˝![]() £¨ πµ√
£¨ πµ√![]() ≥…¡¢£¨«Û µ ˝
≥…¡¢£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∂˛¥Œ∫Ø ˝f£®x£©=ax2+bx+1£¨a£¨b° R£¨µ±x=©Å1 ±£¨∫Ø ˝f£®x£©»°µΩ◊Ó–°÷µ£¨«“◊Ó–°÷µŒ™0£ª
£®1£©«Ûf£®x£©Ω‚Œˆ Ω£ª
£®2£©πÿ”⁄xµƒ∑Ω≥Ãf£®x£©=|x+1|©Åk+3«°”–¡Ω∏ˆ≤ªœ‡µ»µƒ µ ˝Ω‚£¨«Û µ ˝kµƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øº◊°¢““¡Ωº“…Ã≥°∂‘Õ¨“ª÷÷…Ã∆∑ø™’π¥Ÿœ˙ªÓ∂Ø£¨∂‘π∫¬Ú∏√…Ã∆∑µƒπÀøÕ¡Ωº“…Ã≥°µƒΩ±¿¯∑Ω∞∏»Áœ¬£∫
º◊…Ã≥°£∫πÀøÕ◊™∂Ø»ÁÕºÀ˘ æ‘≤≈㨵±÷∏’Î÷∏œÚ“ı”∞≤ø∑÷(Õº÷–Àƒ∏ˆ“ı”∞≤ø∑÷æ˘Œ™…»–Œ£¨«“√ø∏ˆ…»–Œ‘≤–ƒΩ«æ˘Œ™15°„£¨±flΩÁ∫ˆ¬‘≤ªº∆) º¥Œ™÷–Ω±.

““…Ã≥°£∫¥”◊∞”–3∏ˆ∞◊«Ú3∏ˆ∫Ï«Úµƒ∫–◊”÷–“ª¥Œ–‘√˛≥ˆ2∏ˆ«Ú(«Ú≥˝—’…´Õ‚≤ªº”«¯∑÷)£¨»Áπ˚√˛µΩµƒ «2∏ˆ∫Ï«Ú£¨º¥Œ™÷–Ω±.
Œ £∫π∫¬Ú∏√…Ã∆∑µƒπÀøÕ‘⁄ƒƒº“…Ã≥°÷–Ω±µƒø…ƒ‹–‘¥Û£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™¡ÀΩ‚ƒ≥–£∏fl»˝—ß…˙µƒ ”¡¶«Èøˆ£¨Àʪ˙µÿ≥È≤È¡À∏√–£100√˚∏fl»˝—ß…˙µƒ ”¡¶«Èøˆ£¨µ√µΩ∆µ¬ ∑÷≤º÷±∑ΩÕº»Áœ¬Õº£¨”…”⁄≤ª…˜Ω´≤ø∑÷ ˝æ›∂™ ߣ¨µ´÷™µ¿«∞4◊ȵƒ∆µ ˝≥…µ»±» ˝¡–£¨∫Û6◊ȵƒ∆µ ˝≥…µ»≤Ó ˝¡–£¨…Ë◊Ó¥Û∆µ¬ Œ™a£¨ ”¡¶‘⁄4.6µΩ5.0÷ƺ‰µƒ—ß…˙ ˝Œ™b£¨‘Úa£¨bµƒ÷µ∑÷±Œ™ (°° °°)
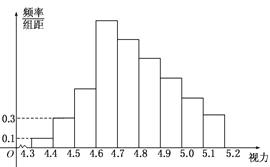
A. 0.27,78 B. 0.27,83 C. 2.7,78 D. 2.7,83
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤![]() £∫
£∫ ![]() £®
£®![]() £©µƒ¿Î–ƒ¬ Œ™
£©µƒ¿Î–ƒ¬ Œ™![]() £¨“‘Õ÷‘≤µƒÀƒ∏ˆ∂•µ„Œ™∂•µ„µƒÀƒ±fl–Œµƒ√ʪ˝Œ™8.
£¨“‘Õ÷‘≤µƒÀƒ∏ˆ∂•µ„Œ™∂•µ„µƒÀƒ±fl–Œµƒ√ʪ˝Œ™8.
£®¢Ò£©«ÛÕ÷‘≤![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®¢Ú£©»ÁÕº£¨–±¬ Œ™![]() µƒ÷±œfl
µƒ÷±œfl![]() ”ÎÕ÷‘≤
”ÎÕ÷‘≤![]() Ωª”⁄
Ωª”⁄![]() £¨
£¨ ![]() ¡Ωµ„£¨µ„
¡Ωµ„£¨µ„![]() ‘⁄÷±œfl
‘⁄÷±œfl![]() µƒ◊Û…œ∑Ω.»Ù
µƒ◊Û…œ∑Ω.»Ù![]() £¨«“÷±œfl
£¨«“÷±œfl![]() £¨
£¨ ![]() ∑÷±”Î
∑÷±”Î![]() ÷·Ωª”⁄
÷·Ωª”⁄![]() £¨
£¨ ![]() µ„£¨«Ûœfl∂Œ
µ„£¨«Ûœfl∂Œ![]() µƒ≥§∂».
µƒ≥§∂».

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™![]() «π´≤Ó≤ªŒ™¡„µƒµ»≤Ó ˝¡–£¨
«π´≤Ó≤ªŒ™¡„µƒµ»≤Ó ˝¡–£¨![]() £¨«“
£¨«“![]() £¨
£¨![]() £¨
£¨![]() ≥…µ»±» ˝¡–£Æ
≥…µ»±» ˝¡–£Æ
£®1£©«Û ˝¡–![]() µƒÕ®œÓ£ª
µƒÕ®œÓ£ª
£®2£©«Û ˝¡–![]() µƒ«∞
µƒ«∞![]() œÓ∫Õ
œÓ∫Õ![]() £Æ
£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤![]() µƒ¿Î–ƒ¬ Œ™
µƒ¿Î–ƒ¬ Œ™![]() £¨«“π˝µ„
£¨«“π˝µ„![]() £Æ
£Æ
£®¢Ò£©«ÛÕ÷‘≤![]() µƒ∑Ω≥ãÆ
µƒ∑Ω≥ãÆ
£®¢Ú£©»Ù![]() £¨
£¨ ![]() «Õ÷‘≤
«Õ÷‘≤![]() …œ¡Ω∏ˆ≤ªÕ¨µƒ∂ص„£¨«“ π
…œ¡Ω∏ˆ≤ªÕ¨µƒ∂ص„£¨«“ π![]() µƒΩ«∆Ω∑÷œfl¥π÷±”⁄
µƒΩ«∆Ω∑÷œfl¥π÷±”⁄![]() ÷·£¨ ‘≈–∂œ÷±œfl
÷·£¨ ‘≈–∂œ÷±œfl![]() µƒ–±¬ «∑ÒŒ™∂®÷µ£ø»Ù «£¨«Û≥ˆ∏√÷µ£ª»Ù≤ª «£¨Àµ√˜¿Ì”…£Æ
µƒ–±¬ «∑ÒŒ™∂®÷µ£ø»Ù «£¨«Û≥ˆ∏√÷µ£ª»Ù≤ª «£¨Àµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™”≠Ω”2017ƒÍ°∞À´![]() °±£¨°∞À´
°±£¨°∞À´![]() °±π∫ŒÔøÒª∂Ω⁄µƒ¿¥¡Ÿ£¨ƒ≥«‡ª®¥……˙≤˙≥ߺ“º∆ªÆ√øÃÏ…˙≤˙ÿÕΰ¢ª®∆ø°¢≤˱≠’‚»˝÷÷¥…∆˜π≤
°±π∫ŒÔøÒª∂Ω⁄µƒ¿¥¡Ÿ£¨ƒ≥«‡ª®¥……˙≤˙≥ߺ“º∆ªÆ√øÃÏ…˙≤˙ÿÕΰ¢ª®∆ø°¢≤˱≠’‚»˝÷÷¥…∆˜π≤![]() ∏ˆ£¨…˙≤˙“ª∏ˆÃ¿ÕΖË
∏ˆ£¨…˙≤˙“ª∏ˆÃ¿ÕΖË![]() ∑÷÷”£¨…˙≤˙“ª∏ˆª®∆ø–Ë
∑÷÷”£¨…˙≤˙“ª∏ˆª®∆ø–Ë![]() ∑÷÷”£¨…˙≤˙“ª∏ˆ≤˱≠–Ë
∑÷÷”£¨…˙≤˙“ª∏ˆ≤˱≠–Ë![]() ∑÷÷”£¨“—÷™◊‹…˙≤˙ ±º‰≤ª≥¨π˝
∑÷÷”£¨“—÷™◊‹…˙≤˙ ±º‰≤ª≥¨π˝![]() –° ±£Æ»Ù…˙≤˙“ª∏ˆÃ¿ÕÎø…ªÒ¿˚»Û
–° ±£Æ»Ù…˙≤˙“ª∏ˆÃ¿ÕÎø…ªÒ¿˚»Û![]() ‘™£¨…˙≤˙“ª∏ˆª®∆øø…ªÒ¿˚»Û
‘™£¨…˙≤˙“ª∏ˆª®∆øø…ªÒ¿˚»Û![]() ‘™£¨…˙≤˙“ª∏ˆ≤˱≠ø…ªÒ¿˚»Û
‘™£¨…˙≤˙“ª∏ˆ≤˱≠ø…ªÒ¿˚»Û![]() ‘™£Æ
‘™£Æ
£®1£© π”√√øÃÏ…˙≤˙µƒÃ¿ÕÎ∏ˆ ˝![]() ”Ϊ®∆ø∏ˆ ˝
”Ϊ®∆ø∏ˆ ˝![]() ±Ì æ√øÃϵƒ¿˚»Û
±Ì æ√øÃϵƒ¿˚»Û![]() £®‘™£©£ª
£®‘™£©£ª
£®2£©‘ı—˘∑÷≈‰…˙≤˙»ŒŒÒ≤≈ƒ‹ π√øÃϵƒ¿˚»Û◊Ó¥Û£¨◊Ó¥Û¿˚»Û «∂‡…Ÿ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com