
【题目】设向量![]() ,
,![]() ,令函数
,令函数![]() ,若函数
,若函数![]() 的部分图象如图所示,且点
的部分图象如图所示,且点![]() 的坐标为
的坐标为![]() .
.

(1)求点![]() 的坐标;
的坐标;
(2)求函数![]() 的单调增区间及对称轴方程;
的单调增区间及对称轴方程;
(3)若把方程![]() 的正实根从小到大依次排列为
的正实根从小到大依次排列为![]() ,求
,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】某工厂新研发了一种产品,该产品每件成本为5元,将该产品按事先拟定的价格进行销售,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求销量![]() (件)关于单价
(件)关于单价![]() (元)的线性回归方程
(元)的线性回归方程![]() ;
;
(2)若单价定为10元,估计销量为多少件;
(3)根据销量![]() 关于单价
关于单价![]() 的线性回归方程,要使利润
的线性回归方程,要使利润![]() 最大,应将价格定为多少?
最大,应将价格定为多少?
参考公式: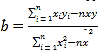 ,
,![]() .参考数据:
.参考数据:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王每天自己开车上班,他在路上所用的时间![]() (分钟)与道路的拥堵情况有关.小王在一年中随机记录了200次上班在路上所用的时间,其频数统计如下表,用频率近似代替概率.
(分钟)与道路的拥堵情况有关.小王在一年中随机记录了200次上班在路上所用的时间,其频数统计如下表,用频率近似代替概率.
| 15 | 20 | 25 | 30 |
频数(次) | 50 | 50 | 60 | 40 |
(Ⅰ)求小王上班在路上所用时间的数学期望![]() ;
;
(Ⅱ)若小王一周上班5天,每天的道路拥堵情况彼此独立,设一周内上班在路上所用时间不超过![]() 的天数为
的天数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某工厂生产线上随机抽取16件零件,测量其内径数据从小到大依次排列如下(单位:![]() ):1.12,1.15,1.21,1.23,1.25,1.25,1.26,1.30,1.30,1.32,1.34,1.35,1.37,1.38,1.41,1.42,据此可估计该生产线上大约有25%的零件内径小于等于_____
):1.12,1.15,1.21,1.23,1.25,1.25,1.26,1.30,1.30,1.32,1.34,1.35,1.37,1.38,1.41,1.42,据此可估计该生产线上大约有25%的零件内径小于等于_____![]() ,大约有30%的零件内径大于_____
,大约有30%的零件内径大于_____![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调递增区间;
的单调递增区间;
(2)对于![]() ,
,![]() 为任意实数,关于
为任意实数,关于![]() 的方程
的方程![]() 恰好有两个不等实根,求实数
恰好有两个不等实根,求实数![]() 的值;
的值;
(3)在(2)的条件下,若不等式![]() 在
在![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(x0 , 0),B(0,y0)两点分别在x轴和y轴上运动,且|AB|=1,若动点P(x,y)满足 ![]() .
.
(1)求出动点P的轨迹对应曲线C的标准方程;
(2)一条纵截距为2的直线l1与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程;
(3)直线l2:x=ty+1与曲线C交于A、B两点,E(1,0),试问:当t变化时,是否存在一直线l2 , 使△ABE的面积为 ![]() ?若存在,求出直线l2的方程;若不存在,说明理由.
?若存在,求出直线l2的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com