
【题目】已知射手甲射击一次,命中9环(含9环)以上的概率为0.56,命中8环的概率为0.22,命中7环的概率为0.12.
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)求甲射击一次,命中不足8环的概率;
(2)求甲射击一次,至少命中7环的概率.
【答案】(1)甲射击一次,命中不足8环的概率是0.22.
(2)甲射击一次,至少命中7环的概率为0.9
【解析】
记“甲射击一次,命中7环以下”为事件A,“甲射击一次,命中7环”为事件B,由于在一次射击中,A与B不可能同时发生,故A与B是互斥事件.
(1)“甲射击一次,命中不足8环”的事件为A+B,由互斥事件的概率加法公式,能求出甲射击一次,命中不足8环的概率.
(2)方法1:记“甲射击一次,命中8环”为事件C,“甲射击一次,命中9环(含9环)以上”为事件D,则“甲射击一次,至少命中7环”的事件为B+C+D,由此能求出甲射击一次,至少命中7环的概率.
方法2:“甲射击一次,至少命中7环”为事件![]() ,由对立事件的概率求法能求出甲射击一次,至少命中7环的概率.
,由对立事件的概率求法能求出甲射击一次,至少命中7环的概率.
记“甲射击一次,命中7环以下”为事件A,则P(A)=1﹣0.56﹣0.22﹣0.12=0.1,
“甲射击一次,命中7环”为事件B,则P(B)=0.12,
由于在一次射击中,A与B不可能同时发生,
故A与B是互斥事件,
(1)“甲射击一次,命中不足8环”的事件为A+B,
由互斥事件的概率加法公式,
P(A+B)=P(A)+P(B)=0.1+0.12=0.22.
答:甲射击一次,命中不足8环的概率是0.22.
(2)方法1:记“甲射击一次,命中8环”为事件C,
“甲射击一次,命中9环(含9环)以上”为事件D,
则“甲射击一次,至少命中7环”的事件为B+C+D,
∴P(B+C+D)=P(B)+P(C)+P(D)=0.12+0.22+0.56=0.9.
答:甲射击一次,至少命中7环的概率为0.9.
方法2:∵“甲射击一次,至少命中7环”为事件![]() ,
,
∴![]() 1﹣0.1=0.9.
1﹣0.1=0.9.
答:甲射击一次,至少命中7环的概率为0.9.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求函数![]() 在区间
在区间![]() 上的值域
上的值域
(2)把函数![]() 图象所有点的上横坐标缩短为原来的
图象所有点的上横坐标缩短为原来的![]() 倍,再把所得的图象向左平移
倍,再把所得的图象向左平移![]() 个单位长度
个单位长度![]() ,再把所得的图象向下平移1个单位长度,得到函数
,再把所得的图象向下平移1个单位长度,得到函数![]() , 若函数
, 若函数![]() 关于点
关于点![]() 对称
对称
(i)求函数![]() 的解析式;
的解析式;
(ii)求函数![]() 单调递增区间及对称轴方程.
单调递增区间及对称轴方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年1月8日,中共中央国务院隆重举行国家科学技术奖励大会,在科技界引发热烈反响,自主创新正成为引领经济社会发展的强劲动力.某科研单位在研发新产品的过程中发现了一种新材料,由大数据测得该产品的性能指标值y与这种新材料的含量x(单位:克)的关系为:当![]() 时,y是x的二次函数;当
时,y是x的二次函数;当![]() 时,
时,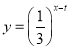 测得数据如下表(部分):
测得数据如下表(部分):
x(单位:克) | 0 | 1 | 2 | 9 | … |
y | 0 |
| 3 |
| … |
(1)求y关于x的函数关系式![]() ;
;
(2)当该产品中的新材料含量x为何值时,产品的性能指标值最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足以下两个条件:①不等式
满足以下两个条件:①不等式![]() 的解集是
的解集是![]() ②函数
②函数![]() 在
在![]() 上的最小值是3.
上的最小值是3.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)若点![]() 在函数
在函数![]() 的图象上,且
的图象上,且![]() .
.
(ⅰ)求证:数列![]() 为等比数列
为等比数列
(ⅱ)令![]() ,是否存在正实数
,是否存在正实数![]() ,使不等式
,使不等式![]() 对于一切的
对于一切的![]() 恒成立?若存在,指出
恒成立?若存在,指出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018届福建省福州市高三上学期期末】过椭圆![]() 的右焦点作
的右焦点作![]() 轴的垂线,交
轴的垂线,交![]() 于
于![]() 两点,直线
两点,直线![]() 过
过![]() 的左焦点和上顶点.若以
的左焦点和上顶点.若以![]() 为直径的圆与
为直径的圆与![]() 存在公共点,则
存在公共点,则![]() 的离心率的取值范围是( )
的离心率的取值范围是( )
A. 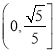 B.
B. 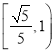 C.
C. 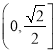 D.
D. 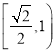
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地建一座桥,两端的桥墩已建好,这两墩相距m米,余下工程只需建两端桥墩之间的桥面和桥墩.经测算,一个桥墩的工程费用为256万元;距离为x米的相邻两墩之间的桥面工程费用为(2+![]() )x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.
)x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.
(1)试写出y关于x的函数关系式;
(2)当m=640米时,需新建多少个桥墩才能使y最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com