
【题目】如图,三棱柱![]() 中,点
中,点![]() 是
是![]() 的中点.
的中点.
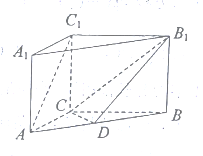
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,求二面角
,求二面角![]() 的大小.
的大小.
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)设函数![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的值域;
上的值域;
(2)定义![]() 表示
表示![]() 中较小者,设函数
中较小者,设函数![]()
![]() .
.
①求函数![]() 的单调区间及最值;
的单调区间及最值;
②若关于![]() 的方程
的方程![]() 有两个不同的实根,求实数
有两个不同的实根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:关于x的方程x2+ax+2=0无实根,命题q:函数f(x)=logax在(0,+∞)上单调递增,若“p∧q”为假命题,“p∨q”真命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,一块形状为四棱柱的木料, ![]() 分别为
分别为![]() 的中点.
的中点.
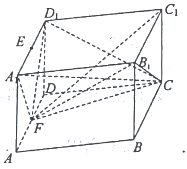
(1)要经过![]() 和
和![]() 将木料锯开,在木料上底面
将木料锯开,在木料上底面![]() 内应怎样画线?请说明理由;
内应怎样画线?请说明理由;
(2)若底面![]() 是边长为2的菱形,
是边长为2的菱形, ![]() ,
, ![]() 平面
平面![]() ,且
,且![]() ,求几何体
,求几何体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 对任意实数
对任意实数![]() 均有
均有![]() ,其中常数
,其中常数![]() 为负数,且
为负数,且![]() 在区间
在区间![]() 上有表达式
上有表达式![]() .
.
(1)写出![]() 在
在![]() 上的表达式,并写出函数
上的表达式,并写出函数![]() 在
在![]() 上的单调区间(不用过程,直接写出即可);
上的单调区间(不用过程,直接写出即可);
(2)求出![]() 在
在![]() 上的最小值与最大值,并求出相应的自变量的取值.
上的最小值与最大值,并求出相应的自变量的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学参加学校自主招生3门课程的考试,假设该同学第一门课程取得优秀成绩概率为 ![]() ,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
ξ | 0 | 1 | 2 | 3 |
p |
| x | y |
|
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率及求p,q的值;
(Ⅱ)求该生取得优秀成绩课程门数的数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() :
: ![]() 的离心率为
的离心率为 ![]() ,且过点
,且过点 ![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆 ![]() 上异于长轴端点的两点.
上异于长轴端点的两点.
(1)求椭圆 ![]() 的方程;
的方程;
(2)已知直线 ![]() :
: ![]() ,且
,且 ![]() ,垂足为
,垂足为 ![]() ,
, ![]() ,垂足为
,垂足为 ![]() ,若
,若 ![]() ,且
,且 ![]() 的面积是
的面积是 ![]() 面积的5倍,求
面积的5倍,求 ![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com