练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在正方体中，有下列结论：

    ①平面；

    ②异面直线AD与所成的角为；

    ③三棱柱的体积是三棱锥的体积的四倍；

    ④在四面体中，分别连接三组对棱的中点的线段互相垂直平分.

    其中正确的是________（填出所有正确结论的序号）.

    【答案】①④

    【解析】

    根据正方体的几何特征，证明线面平行，求异面直线夹角，求体积关系，分析正四面体对棱连线特点.

    因为，平面，平面，所以平面，故①正确；

    因为，所以异面直线AD与所成的角等于，在正方形中，，故②错误；

    三棱柱的体积是三棱锥的体积的三倍，故③错误；

    由正方体的性质可知，正方体三条对面中心连线线段相互垂直平分.

    四面体是正四面体，其棱中点即正方体每个面的中心，对棱中点连线必经过正方体的中心，由对称性知，连接正四面体每组对棱中点的线段互相垂直平分，则④正确.

    故答案为：①④

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数满足：①对任意实数都有；②对任意，都有恒成立；③不恒为0，且当时，.

    （1）求的值；

    （2）判断函数的奇偶性，并给出你的证明.

    （3）定义“若存在非零常数，使得对函数定义域中的任意一个，均有，则称为以为周期的周期函数”.试证明：函数为周期函数，并求出的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表，即杨辉三角，这是数学史上的一个伟大成就.在“杨辉三角”中，第行的所有数字之和为，若去除所有为1的项，依次构成数列，则此数列的前55项和为( )

    A. 4072B. 2026C. 4096D. 2048

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在四棱锥S—ABCD中，SA⊥平面ABCD，底面ABCD为直角梯形，其中AB∥CD，∠ADC＝90°，AD＝AS＝2，AB＝1，CD＝3，点E在棱CS上，且CE＝λCS．

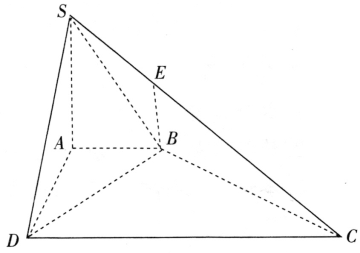
    （1）若，证明：BE⊥CD；

    （2）若，求点E到平面SBD的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】A，B，C，D是空间不共面的四点，它们到平面a的距离之比依次为1：1：1：2，则满足条件的平面a的个数是：

    A. 1 B. 4 C. 7 D. 8.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，对称轴为直线的抛物线经过点和.

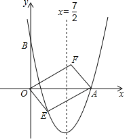
    （1）求抛物线解析式及顶点坐标；

    （2）设点是抛物线上一动点，且位于第四象限，四边形OEAF是以OA为对角线的平行四边形，求四边形OEAF的面积S与x之间的函数关系式，并写出自变量x的取值范围；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求函数的单调增区间；

    （2）若不等式对于任意成立，求正实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的焦点为，准线为，若点在上，点在上，且是周长为的正三角形．

    （1）求的方程；

    （2）过点的直线与抛物线相交于两点，抛物线在点处的切线与交于点，求面积的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在底面是菱形的四棱锥中，，，，点在上，且.

    （1）点在棱上且平面，求线段的长度；

    （2）在（1）的条件下，求点到平面的距离.

    查看答案和解析>>

    同步练习册答案