Question

【题目】定义：对于函数，若在定义域内存在实数，满足，则称为“局部奇函数”．

（1）已知二次函数，试判断是否为定义域上的“局部奇函数”?若是，求出所有满足的的值；若不是，请说明事由．

（2）若是定义在区间上的“局部奇函数”，求实数的取值范围．

（3）若为定义域上的“局部奇函数”，求实数的取值范围．

Answer 1

【答案】（1）f（x）为“局部奇函数”．（2）m∈[﹣，﹣1]．（3）1﹣≤m≤2．

【解析】

试题（1）利用局部奇函数的定义，建立方程关系，然后判断方程是否有解，有解则是“局部奇函数”，若无解，则不是；（2）（3）都是利用“局部奇函数的定义”，建立方程关系，并将方程有解的问题转化成二次方程根的分布问题，从而求出各小问参数的取值范围.

试题解析：（1）当，方程即，有解

所以为“局部奇函数”

（2）法一：当时，可化为

因为的定义域为，所以方程在上有解

令，则，设，则在上为减函数，在上为增函数，所以当时，，所以，即；

法二：当时，可化为

因为的定义域为，所以方程即在上有解

令，则关于的二次方程在上有解即可保证为“局部奇函数”

设，当方程在上只有一解时，须满足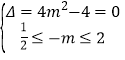或，解之得（舍去，因为此时方程在区间有两解，不符合这种情况）或；

当方程在上两个不等的实根时，须满足

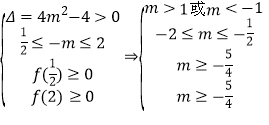
，综上可知；

（3）当为定义域上的“局部奇函数”时

,可化为，

令则,

从而在有解,即可保证为“局部奇函数”

令，则

①当时,在有解,即,解得

②当时,在有解等价于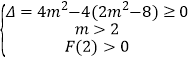

解得;综上可知.