
【题目】随着“互联网+交通”模式的迅猛发展,“共享自行车”在很多城市相继出现.某运营公司为了了解某地区用户对其所提供的服务的满意度,随机调查了40个用户,得到用户的满意度评分如下:
用户编号 | 评分 | 用户编号 | 评分 | 用户编号 | 评分 | 用户编号 | 评分 |
01 | 78 | 11 | 88 | 21 | 79 | 31 | 93 |
02 | 73 | 12 | 86 | 22 | 83 | 32 | 78 |
03 | 81 | 13 | 95 | 23 | 72 | 33 | 75 |
04 | 92 | 14 | 76 | 24 | 74 | 34 | 81 |
05 | 95 | 15 | 97 | 25 | 91 | 35 | 84 |
06 | 85 | 16 | 78 | 26 | 66 | 36 | 77 |
07 | 79 | 17 | 88 | 27 | 80 | 37 | 81 |
08 | 84 | 18 | 82 | 28 | 83 | 38 | 76 |
09 | 63 | 19 | 76 | 29 | 74 | 39 | 85 |
10 | 86 | 20 | 89 | 30 | 82 | 40 | 89 |
现用随机数法读取用户编号,且从第2行第6列的数开始向右读,从40名用户中抽取容量为10的样本.(下面是随机数表第1行第至第5行)
95 33 95 22 00 18 74 72 00 18 38 79 58 69 32
81 76 80 16 92 04 80 44 25 39 91 03 69 79 83
54 31 62 27 32 94 07 53 89 35 96 35 23 79 18
05 98 90 07 35 46 40 62 98 80 54 97 20 56 95
(1)请你列出抽到的10个样本的评分数据;
(2)计算所抽到的10个样本的均值![]() 和方差
和方差![]() ;
;
(3)在(2)条件下,若用户的满意度评分在![]() 之间,则满意度等级为“
之间,则满意度等级为“![]() 级”.试应用样本估计总体的思想,根据所抽到的10个样本,估计该地区满意度等级为“
级”.试应用样本估计总体的思想,根据所抽到的10个样本,估计该地区满意度等级为“![]() 级”的用户所占的百分比是多少?(参考数据:
级”的用户所占的百分比是多少?(参考数据:![]() )
)
【答案】(1)见解析;(2)均值![]() ,方差
,方差![]() ;(3)
;(3)![]()
【解析】
(1)通过系统抽样得到抽取的样本编号,从而得到样本的评分数据.
(2)由(1)中的样本评分数据利用平均数和方差公式求解.
(3)由(2)得到满意度等级, 得到由(1)中容量为10的样本评分在![]() 之间的人数,然后求得百分比.
之间的人数,然后求得百分比.
(1)通过系统抽样抽取的样本编号为:01,20,04,10,36,35,16,22,29,40
则样本的评分数据为:78,89,92,86,77,84,78,83,74,89.
(2)由(1)中的样本评分数据可得
![]()
![]() ,
,
则有![]()
![]()
![]()
所以均值![]() ,方差
,方差![]() .
.
(3)由题意知评分在![]() 即
即![]() 之间满意度等级为“A级”,
之间满意度等级为“A级”,
由(1)中容量为10的样本评分在![]() 之间有5人,
之间有5人,
则该地区满意度等级为“A级”的用户所占的百分比约为![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为 为参数
为参数![]() ,以坐标原点O为极点,以x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为
,以坐标原点O为极点,以x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为![]() .
.
![]() 求直线l的普通方程及曲线C的直角坐标方程;
求直线l的普通方程及曲线C的直角坐标方程;
![]() 若直线l与曲线C交于A,B两点,求线段AB的中点P到坐标原点O的距离.
若直线l与曲线C交于A,B两点,求线段AB的中点P到坐标原点O的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费10元;重量超过
的包裹收费10元;重量超过![]() 的包裹,除收费10元之外,超过
的包裹,除收费10元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需要再收费5元.该公司近60天每天揽件数量的频率分布直方图如下图所示(同一组数据用该区间的中点值作代表).
计算)需要再收费5元.该公司近60天每天揽件数量的频率分布直方图如下图所示(同一组数据用该区间的中点值作代表).
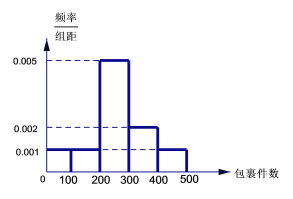
(1)求这60天每天包裹数量的平均值和中位数;
(2)该公司从收取的每件快递的费用中抽取5元作为前台工作人员的工资和公司利润,剩余的作为其他费用.已知公司前台有工作人员3人,每人每天工资100元,以样本估计总体,试估计该公司每天的利润有多少元?
(3)小明打算将![]() 四件礼物随机分成两个包裹寄出,且每个包裹重量都不超过
四件礼物随机分成两个包裹寄出,且每个包裹重量都不超过![]() ,求他支付的快递费为45元的概率.
,求他支付的快递费为45元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两队参加听歌猜歌名游戏,每队![]() 人.随机播放一首歌曲, 参赛者开始抢答,每人只有一次抢答机会,答对者为本队赢得一分,答错得零分, 假设甲队中每人答对的概率均为
人.随机播放一首歌曲, 参赛者开始抢答,每人只有一次抢答机会,答对者为本队赢得一分,答错得零分, 假设甲队中每人答对的概率均为![]() ,乙队中
,乙队中![]() 人答对的概率分别为
人答对的概率分别为![]() ,且各人回答正确与否相互之间没有影响.
,且各人回答正确与否相互之间没有影响.
(1)若比赛前随机从两队的![]() 个选手中抽取两名选手进行示范,求抽到的两名选手在同一个队的概率;
个选手中抽取两名选手进行示范,求抽到的两名选手在同一个队的概率;
(2)用![]() 表示甲队的总得分,求随机变量
表示甲队的总得分,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(3)求两队得分之和大于4的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
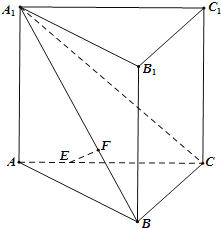
【题目】如图,在直三棱柱![]() 侧棱和底面垂直的棱柱
侧棱和底面垂直的棱柱![]() 中,平面
中,平面![]() 侧面
侧面![]() ,
,![]() ,线段AC、
,线段AC、![]() 上分别有一点E、F且满足
上分别有一点E、F且满足![]() ,
,![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 求点E到直线
求点E到直线![]() 的距离;
的距离;
![]() 求二面角
求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)试探究当![]() 时,方程
时,方程![]() 的解的个数,并说明理由.
的解的个数,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com