【答案】
分析:(I)设a
n=a>0,利用数列{a
n}、{b
n}满足a
nb
n+1+a
n+1b
n=2na
n+1(n∈N
*),可得b
n+1+b
n=2n,(n∈N
*),于是当n≥2时,b
n+b
n-1=2(n-1).于是b
n+1-b
n-1=2.可知:数列{b
n}当n为奇数或偶数时按原顺序均构成以2为公差的等差数列,利用等差数列的通项公式即可得出;
(II)设{a
n}、{b
n}公差分别为d
1、d
2,可得其通项公式,代入a
nb
n+1+a
n+1b
n=2na
n+1(n∈N
*).可得[a
1+(n-1)d
1][b
1+nd
2]+(a
1+nd
1)[b
1+(n-1)d
2]=2n(a
1+nd
1),对于任意n恒成立,可得
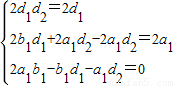
,解出即可;
(III)利用
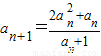
,可得a
n+1-a
n=
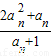
-a
n=
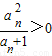
,于是a
n<a
n+1.利用a
nb
n+1+a
n+1b
n=2na
n+1<a
n+1b
n+1+a
n+1b
n,可得2n<b
n+1+b
n.又a
nb
n+1=(2n-b
n)•a
n+1>0,a
n+1>0,可得2n-b
n>0.可得
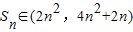
,进而得出.
解答:(I)解:设a
n=a>0,∵数列{a
n}、{b
n}满足a
nb
n+1+a
n+1b
n=2na
n+1(n∈N
*),
∴b
n+1+b
n=2n,(n∈N
*),于是当n≥2时,b
n+b
n-1=2(n-1).
∴b
n+1-b
n-1=2.
∴可知:数列{b
n}当n为奇数或偶数时按原顺序均构成以2为公差的等差数列,
又
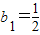
,b
1+b
2=2,可得
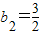
.
∴
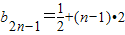
=
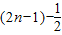
,
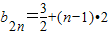
=
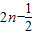
,
即
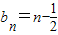
(n∈N
*).
(2)证明:设{a
n}、{b
n}公差分别为d
1、d
2,
则a
n=a
1+(n-1)d,b
n=b
1+(n-1)d
2,
代入a
nb
n+1+a
n+1b
n=2na
n+1(n∈N
*).
可得[a
1+(n-1)d
1][b
1+nd
2]+(a
1+nd
1)[b
1+(n-1)d
2]=2n(a
1+nd
1),对于任意n恒成立,
可得
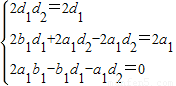
,解得
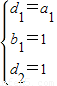
,
可得a
n=na
1,b
n=n.
∴只有取a
1>0可得数列{a
n}有无穷多个,而数列{b
n}惟一确定;
(3)证明:∵
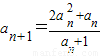
,
∴a
n+1-a
n=
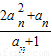
-a
n=
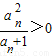
,
∴a
n<a
n+1.
∴a
nb
n+1+a
n+1b
n=2na
n+1<a
n+1b
n+1+a
n+1b
n,可得2n<b
n+1+b
n.
因此
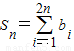
=(b
1+b
2)+(b
3+b
4)+…+(b
2n-1+b
2n)>2[1+3+…+(2n-1)]=2n
2.
又a
nb
n+1=(2n-b
n)•a
n+1>0,a
n+1>0,
∴2n-b
n>0.
∴
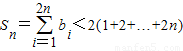
=2n(1+2n)=4n
2+2n,
∴
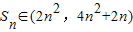
,
∴
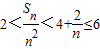
.
点评:熟练掌握等差数列的通项公式及其前n项和公式、数列的单调性、放缩法等是解题的关键.

 时,求数列{bn}的通项公式;
时,求数列{bn}的通项公式; ,Sn=
,Sn=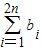 ,求证:2<
,求证:2<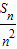 <6.
<6.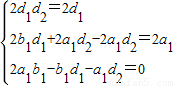 ,解出即可;
,解出即可;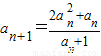 ,可得an+1-an=
,可得an+1-an=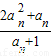 -an=
-an=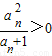 ,于是an<an+1.利用anbn+1+an+1bn=2nan+1<an+1bn+1+an+1bn,可得2n<bn+1+bn.又anbn+1=(2n-bn)•an+1>0,an+1>0,可得2n-bn>0.可得
,于是an<an+1.利用anbn+1+an+1bn=2nan+1<an+1bn+1+an+1bn,可得2n<bn+1+bn.又anbn+1=(2n-bn)•an+1>0,an+1>0,可得2n-bn>0.可得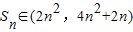 ,进而得出.
,进而得出.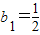 ,b1+b2=2,可得
,b1+b2=2,可得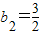 .
.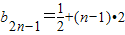 =
=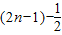 ,
,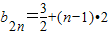 =
=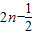 ,
,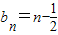 (n∈N*).
(n∈N*).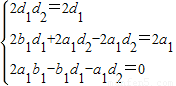 ,解得
,解得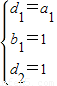 ,
,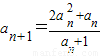 ,
,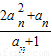 -an=
-an=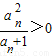 ,
,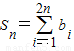 =(b1+b2)+(b3+b4)+…+(b2n-1+b2n)>2[1+3+…+(2n-1)]=2n2.
=(b1+b2)+(b3+b4)+…+(b2n-1+b2n)>2[1+3+…+(2n-1)]=2n2.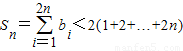 =2n(1+2n)=4n2+2n,
=2n(1+2n)=4n2+2n,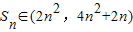 ,
,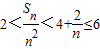 .
.
