
【题目】如图,某地三角工厂分别位于边长为2的正方形![]() 的两个顶点
的两个顶点![]() 及
及![]() 中点
中点![]() 处.为处理这三角工厂的污水,在该正方形区域内(含边界)与
处.为处理这三角工厂的污水,在该正方形区域内(含边界)与![]() 等距的点
等距的点![]() 处建一个污水处理厂,并铺设三条排污管道
处建一个污水处理厂,并铺设三条排污管道![]() ,记辅设管道总长为
,记辅设管道总长为![]() 千米.
千米.
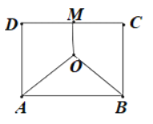
(1)按下列要求建立函数关系式:
(i)设![]() ,将
,将![]() 表示成
表示成![]() 的函数;
的函数;
(ii)设![]() ,将
,将![]() 表示成
表示成![]() 的函数;
的函数;
(2)请你选用一个函数关系,确定污水厂位置,使铺设管道总长最短.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】若数列![]() 满足:对于
满足:对于![]() ,都有
,都有![]() (
(![]() 为常数),则称数列
为常数),则称数列![]() 是公差为
是公差为![]() 的“隔项等差”数列.
的“隔项等差”数列.
(Ⅰ)若![]() ,
,![]() 是公差为8的“隔项等差”数列,求
是公差为8的“隔项等差”数列,求![]() 的前
的前![]() 项之和;
项之和;
(Ⅱ)设数列![]() 满足:
满足:![]() ,对于
,对于![]() ,都有
,都有![]() .
.
①求证:数列![]() 为“隔项等差”数列,并求其通项公式;
为“隔项等差”数列,并求其通项公式;
②设数列![]() 的前
的前![]() 项和为
项和为![]() ,试研究:是否存在实数
,试研究:是否存在实数![]() ,使得
,使得![]() 成等比数列(
成等比数列(![]() )?若存在,请求出
)?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
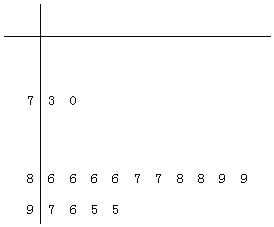
【题目】陕西理工大学开展大学生社会实践活动,用“10分制”随机调查汉台区某社区居民的幸福指数,现从调查人群中随机抽取16人,如图所示的茎叶图记录了他们的幸福指数的得分![]() 以小数点的前一位数字为茎,小数点后的一位数字为叶
以小数点的前一位数字为茎,小数点后的一位数字为叶![]() :
:
![]() 写出这组数据的众数和中位数;
写出这组数据的众数和中位数;
![]() 若幸福指数不低于9分,则称该人的幸福指数为“极幸福”;若幸福指数不高于8分,则称该人的幸福指数为“不够幸福”
若幸福指数不低于9分,则称该人的幸福指数为“极幸福”;若幸福指数不高于8分,则称该人的幸福指数为“不够幸福”![]() 现从这16人中幸福指数为“极幸福”和“不够幸福”的人中任意选取2人,求选出的两人的幸福指数均为“极幸福”的概率.
现从这16人中幸福指数为“极幸福”和“不够幸福”的人中任意选取2人,求选出的两人的幸福指数均为“极幸福”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-mlnx,h(x)=x2-x+a.
(1)当a=0时,f(x)≥h(x)在(1,+∞)上恒成立,求实数m的取值范围;
(2)当m=2时,若函数k(x)=f(x)-h(x)在区间(1,3)上恰有两个不同零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+e-x,g(x)=2x+ax3,a为实常数.
(1)求g(x)的单调区间;
(2)当a=-1时,证明:存在x0∈(0,1),使得y=f(x)和y=g(x)的图象在x=x0处的切线互相平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成![]() 两组,每组100只,其中
两组,每组100只,其中![]() 组小鼠给服甲离子溶液,
组小鼠给服甲离子溶液,![]() 组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:

记![]() 为事件:“乙离子残留在体内的百分比不低于
为事件:“乙离子残留在体内的百分比不低于![]() ”,根据直方图得到
”,根据直方图得到![]() 的估计值为
的估计值为![]() .
.
(1)求乙离子残留百分比直方图中![]() 的值;
的值;
(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com