
【题目】已知定义域为![]() 的单调减函数
的单调减函数![]() 是奇函数,当
是奇函数,当![]() 时,
时,![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求![]() 的解析式;
的解析式;
(Ⅲ)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(I)![]() ;(II)
;(II)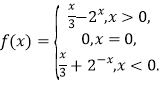 ;(III)
;(III)![]() .
.
【解析】
(Ⅰ)利用定义域为R的函数f(x)是奇函数,求f(0)的值;
(Ⅱ)求出x<0的解析式,即可求f(x)的解析式;
(Ⅲ)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,f(x)在R上是减函数,所以t2﹣2t>k﹣2t2.即3t2﹣2t﹣k>0对任意t∈R恒成立,利用判别式小于0即可求实数k的取值范围.
(Ⅰ)因为定义域为![]() 的函数
的函数![]() 是奇函数,
是奇函数,
所以![]() .
.
(Ⅱ)因为当![]() 时,
时,![]() ,
,
所以![]() .
.
又因为函数![]() 是奇函数,所以
是奇函数,所以![]() .
.
所以![]() .
.
综上,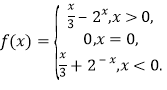
(Ⅲ)由![]() 得
得![]() .
.
因为![]() 是奇函数,
是奇函数,
所以![]() .
.
又![]() 在
在![]() 上是减函数,所以
上是减函数,所以![]() .
.
即![]() 对任意
对任意![]() 恒成立.
恒成立.
令![]() ,则
,则![]() .由
.由![]() ,解得
,解得![]() .
.
故实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣x2﹣ax.
(1)若曲线y=f(x)在点x=0处的切线斜率为1,求函数f(x)在[0,1]上的最值;
(2)令g(x)=f(x)+ ![]() (x2﹣a2),若x≥0时,g(x)≥0恒成立,求实数a的取值范围;
(x2﹣a2),若x≥0时,g(x)≥0恒成立,求实数a的取值范围;
(3)当a=0且x>0时,证明f(x)﹣ex≥xlnx﹣x2﹣x+1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,已知
中,已知![]() 都是边长为
都是边长为![]() 的等边三角形,
的等边三角形,![]() 为
为![]() 中点,且
中点,且![]() 平面
平面![]() ,
,![]() 为线段
为线段![]() 上一动点,记
上一动点,记![]() .
.
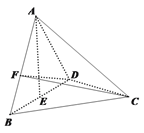
(1)当![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)当![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 在区间
在区间![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,若对任意的
时,若对任意的![]() ,总存在
,总存在![]() 使
使![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 的值域为区间
的值域为区间![]() ,是否存在常数
,是否存在常数![]() ,使区间
,使区间![]() 的长度为
的长度为![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,请说明理由.(柱:区间
的值,若不存在,请说明理由.(柱:区间![]() 的长度为
的长度为![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为Aa,b,c,且满足 ![]() =
= ![]()
(1)若4sinC=c2sinB,求△ABC的面积;
(2)若 ![]()
![]() +
+ ![]() =4,求a的最小值.
=4,求a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式x2+y2≤4确定的平面区域为U,|x|+|y|≤1确定的平面区域为V.
(1)定义横、纵坐标为整数的点为“整点”,在区域U内任取3个整点,求这些整点中恰有2个整点在区域V的概率;
(2)在区域U内任取3个点,记这3个点在区域V的个数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中.侧梭长均为4.底边AC=4.AB=2,BC=2 ![]() ,D.E分别为PC.BC的中点. 〔I)求证:平面PAC⊥平面ABC.
,D.E分别为PC.BC的中点. 〔I)求证:平面PAC⊥平面ABC.
(Ⅱ)求三棱锥P﹣ABC的体积;
(Ⅲ)求二面角C﹣AD﹣E的余弦值.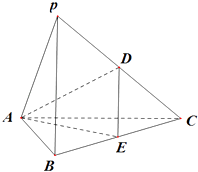
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某镇在政府“精准扶贫”的政策指引下,充分利用自身资源,大力发展养殖业,以增加收入,政府计划共投入72万元,全部用于甲、乙两个合作社,每个合作社至少要投入15万元,其中甲合作社养鱼,乙合作社养鸡,在对市场进行调研分析发现养鱼的收益![]() 、养鸡的收益
、养鸡的收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]()
![]() .设甲合作社的投入为
.设甲合作社的投入为![]() (单位:万元).两个合作社的总收益为
(单位:万元).两个合作社的总收益为![]() (单位:万元).
(单位:万元).
(1)当甲合作社的投入为25万元时,求两个合作社的总收益;
(2)试问如何安排甲、乙两个合作的投入,才能使总收益最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com