Question

利用辗转相除法求7 252与5 328的最大公约数，并用basic语言写出计算机程序.

     

Answer 1

分析：辗转相除法的主要步骤是：（1）用小的一个数除大的一个数，得第一个余数；（2）用第一个余数除小的一个数，得第二个余数；（3）用第二个余数除第一个余数，得第三个余数；（4）逐次用后一个余数去除前一个余数，直到余数为0为止.那么最后一个除数就是所求的最大公约数.

    解：根据上述步骤得：

    7 252=5 328×1+1 924

    5 328=1 924×2+1 480

    1 924=1 480×1+444

    1 480=444×3+148

    444=148×3+0

    最后得到的除数148，即7 252与5 328的最大公约数为148.

    要写出程序，先作出程序框图：

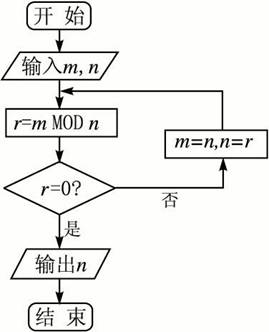
    程序：

    Input “m,n=”;m,n

    r=m MOD n

    While r＜＞0

    m=n

    n=r

    r=m MOD n

    Wend

    Print “最大公约数”；n

    End