
【题目】已知二次函数![]() 在
在![]() 处取得极值,且在
处取得极值,且在![]() 点处的切线与直线
点处的切线与直线![]() 平行.
平行.
(1)求![]() 的解析式;
的解析式;
(2)求函数![]() 的单调递增区间及极值。
的单调递增区间及极值。
(3)求函数![]() 在
在![]() 的最值。
的最值。
【答案】(1)![]() .
.
(2)增区间为![]() ,
,![]() .在
.在![]() 有极小值为0。在
有极小值为0。在![]() 有极大值4/27。
有极大值4/27。
(3)![]() 的最大值为2,最小值为0。
的最大值为2,最小值为0。
【解析】试题分析:(1)第一步,求函数的导数,第二步:根据![]() 处取得极值,知
处取得极值,知![]() ,根据导数的几何意义知;在
,根据导数的几何意义知;在![]() 处的导数等于
处的导数等于![]() ,解得
,解得![]() ,第三步,代入写出
,第三步,代入写出![]() ,令
,令![]() ,得到极值点,最后,解出
,得到极值点,最后,解出![]() ;(2)根据(1)得到的结论,可知
;(2)根据(1)得到的结论,可知![]() 上的单调性,以及极值,比较端点值和极值的大小,就得到最大值和最小值.
上的单调性,以及极值,比较端点值和极值的大小,就得到最大值和最小值.
试题解析:解:(1) 由![]() ,可得
,可得![]() .由题设可得
.由题设可得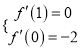
即![]() .解得
.解得![]() ,
, ![]() .所以
.所以![]() .
.
由题意得![]()
所以![]() .
.
令![]() ,得
,得![]() ,
, ![]() .
.
当![]() 变化时,
变化时, ![]() ,
, ![]() 变化情况如下表:
变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
| 单调递增 | 4/27 | 单调递减 | 0 | 单调递增 |
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() .
.
(2)因为在![]() 时函数
时函数![]() 有极小值为0.在
有极小值为0.在![]() 时函数
时函数![]() 有极大值
有极大值![]() .
.
又![]() ,
,
所以函数![]() 的最大值为2,最小值为0.
的最大值为2,最小值为0.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
⑴求椭圆![]() 的标准方程;
的标准方程;
⑵已知动直线![]() 过点
过点![]() 且与椭圆
且与椭圆![]() 交于
交于![]() 两点.试问
两点.试问![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下五个命题:
①在线性回归模型中, ![]() 表示解释变量对于预报变量变化的贡献率,在对女大学生的身高预报体重的回归分析数据中,算得
表示解释变量对于预报变量变化的贡献率,在对女大学生的身高预报体重的回归分析数据中,算得![]() ,表明“女大学生的体重差异有64%是由身高引起的”
,表明“女大学生的体重差异有64%是由身高引起的”
②随机变量的方差和标准差都反映了随机变量取值偏离于均值的平均程度,方差或标准差越小,则随机变量偏离于均值的平均程度越大;
③正态曲线关于直线![]() 对称,这个曲线只有当
对称,这个曲线只有当![]() 时,才在
时,才在![]() 轴上方;
轴上方;
④正态曲线的对称轴由![]() 确定,当
确定,当![]() 一定时,曲线的形状由
一定时,曲线的形状由![]() 决定,并且
决定,并且![]() 越大,曲线越“矮胖”;
越大,曲线越“矮胖”;
⑤若随机变量![]() ,且
,且![]() 则
则![]() ;
;
其中正确命题的序号是
A. ②③ B. ①④⑤ C. ①④ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,双曲线
,双曲线![]() 的一条渐近线与
的一条渐近线与![]() 轴所成的夹角为
轴所成的夹角为![]() ,且双曲线的焦距为
,且双曲线的焦距为![]() .
.
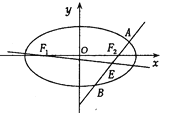
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 分别为椭圆
分别为椭圆![]() 的左,右焦点,过
的左,右焦点,过![]() 作直线
作直线![]() (与
(与![]() 轴不重合)交椭圆于
轴不重合)交椭圆于![]() ,
, ![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(数学文卷·2017届湖北省黄冈市高三上学期期末考试第16题) “中国剩余定理”又称“孙子定理”.1852年英国来华传教伟烈亚利将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”. “中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将2至2017这2016个数中能被3除余1且被5除余1的数按由小到大的顺序排成一列,构成数列![]() ,则此数列的项数为__________.
,则此数列的项数为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com