
【题目】已知![]() ,
,![]() 为双曲线
为双曲线![]() 的左、右焦点,过
的左、右焦点,过![]() 的直线
的直线![]() 与圆
与圆![]() 相切于点
相切于点![]() ,且
,且![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. ![]() B. 2 C. 3 D.
B. 2 C. 3 D. ![]()
【答案】D
【解析】试题分析:设F1,F2为(﹣c,0),(c,0),由直线和圆相切可得d=b,运用点到直线的距离公式,以及三角形的勾股定理,可得b,c的方程,解方程可得双曲线的离心率.
详解:设F1,F2为(﹣c,0),(c,0),
由过F1的直线l与圆x2+y2=b2相切,
可得d=b,过F2
向直线做垂线垂足为N,在直角三角形ONF2中,可得|MF1|=a,OQ=2a,OM=b,Q F2=2b,
即有|MF2|=3|MF1|=3a,
由OM为三角形MF1F2的中线,可得
(2|OM|)2+(|F1F2|)2=2(|MF1|2+|MF2|2),
即为4b2+4c2=2(a2+9a2),
即有c2+b2=5![]() ,再根据
,再根据![]() 得到双曲线的离心率为
得到双曲线的离心率为 ![]() .
.
故选:D .


科目:高中数学 来源: 题型:
【题目】某校社团活动开展有声有色,极大地推动了学生的全面发展,深受学生欢迎,每届高一新生都踊跃报名加入.现已知高一某班有6名男同学和4名女同学参加心理社,在这10名同学中,4名同学初中毕业于同一所学校,其余6名同学初中毕业于其他6所不同的学校.现从这10名同学中随机选取4名同学代表社团参加校际交流(每名同学被选到的可能性相同).
(Ⅰ)求选出的4名同学初中毕业于不同学校的概率;
(Ⅱ)设![]() 为选出的4名同学中女同学的人数,求随机变量
为选出的4名同学中女同学的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一辆汽车从![]() 市出发沿海岸一条笔直公路以每小时
市出发沿海岸一条笔直公路以每小时![]() 的速度向东均速行驶,汽车开动时,在
的速度向东均速行驶,汽车开动时,在![]() 市南偏东方向距
市南偏东方向距![]() 市
市![]() 且与海岸距离为
且与海岸距离为![]() 的海上
的海上![]() 处有一快艇与汽车同时出发,要把一份稿件交给这汽车的司机.
处有一快艇与汽车同时出发,要把一份稿件交给这汽车的司机.
(1)快艇至少以多大的速度行驶才能把稿件送到司机手中?
(2)在(1)的条件下,求快艇以最小速度行驶时的行驶方向与![]() 所成的角.
所成的角.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位:![]() )和年利润
)和年利润![]() (单位:千元)的影响,对近8年的年宣传费
(单位:千元)的影响,对近8年的年宣传费![]() 和年销售量
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 56.3 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中![]() ,
,![]() .
.
(1)根据散点图判断, 与
与![]() 哪一个适宜作为年销售量
哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知这种产品的年利率![]() 与
与![]() ,
,![]() 的关系为
的关系为![]() .根据(Ⅱ)的结果回答下列问题:
.根据(Ⅱ)的结果回答下列问题:
(i)年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
(ii)年宣传费![]() 为何值时,年利率的预报值最大?
为何值时,年利率的预报值最大?
附:对于一组数![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】扎花灯是中国一门传统手艺,逢年过节时常常在大街小巷看到各式各样的美丽花灯。现有一个花灯,它外围轮廓是由两个形状完全相同的抛物线绕着它们自身的对称轴旋转而来(如图),花灯的下顶点为![]() ,上顶点为
,上顶点为![]() ,
,![]() 米,在它的内部放有一个半径为
米,在它的内部放有一个半径为![]() 米的球形灯泡,球心
米的球形灯泡,球心![]() 在轴
在轴![]() 上,且
上,且![]() 米。若球形灯泡的球心
米。若球形灯泡的球心![]() 到四周轮廓上的点的最近距离是在下顶点
到四周轮廓上的点的最近距离是在下顶点![]() 处取到。建立适当的坐标系可得抛物线方程为
处取到。建立适当的坐标系可得抛物线方程为![]() ,则实数
,则实数![]() 的取值范围是_______
的取值范围是_______

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以平面直角坐标系
为参数).以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,设直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,设直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 和直线
和直线![]() 的普通方程;
的普通方程;
(2)设![]() 为曲线
为曲线![]() 上任意一点,求点
上任意一点,求点![]() 到直线
到直线![]() 的距离的最值.
的距离的最值.
【答案】(1)![]() ,
, ![]() ;(2)最大值为
;(2)最大值为![]() ,最小值为
,最小值为![]()
【解析】试题分析:(1)根据参数方程和极坐标化普通方程化法即易得结论![]() 的普通方程为
的普通方程为![]() ;直线
;直线![]() 的普通方程为
的普通方程为![]() .(2)求点到线距离问题可借助参数方程,利用三角函数最值法求解即可故设
.(2)求点到线距离问题可借助参数方程,利用三角函数最值法求解即可故设![]() ,
, ![]()
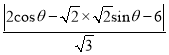
![]()
 .即可得出最值
.即可得出最值
解析:(1)根据题意,由 ,得
,得![]() ,
, ![]() ,
,
由![]() ,得
,得![]() ,
,
故![]() 的普通方程为
的普通方程为![]() ;
;
由![]() 及
及![]() ,
, ![]() 得
得![]() ,
,
故直线![]() 的普通方程为
的普通方程为![]() .
.
(2)由于![]() 为曲线
为曲线![]() 上任意一点,设
上任意一点,设![]() ,
,
由点到直线的距离公式得,点![]() 到直线
到直线![]() 的距离为
的距离为
![]()

![]()
 .
.
∵![]()
![]() ,
,
∴
 ,即
,即![]()
![]() ,
,
故点![]() 到直线
到直线![]() 的距离的最大值为
的距离的最大值为![]() ,最小值为
,最小值为![]() .
.
点睛:首先要熟悉参数方程和极坐标方程化普通方程的方法,第一问基本属于送分题所以务必抓住,对于第二问可以总结为一类题型,借助参数方程设点的方便转化为三角函数最值问题求解
【题型】解答题
【结束】
23
【题目】已知函数![]() ,
,![]() .
.
(1)解关于![]() 的不等式
的不等式![]() ;
;
(2)若函数![]() 的图象恒在函数
的图象恒在函数![]() 图象的上方,求
图象的上方,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业拟用10万元投资甲、乙两种商品.已知各投入![]() 万元,甲、乙两种商品分别可获得
万元,甲、乙两种商品分别可获得![]() 万元的利润,利润曲线
万元的利润,利润曲线![]() ,
,![]() ,如图所示.
,如图所示.

(1)求函数![]() 的解析式;
的解析式;
(2)应怎样分配投资资金,才能使投资获得的利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com