
| A. | $\frac{{\sqrt{3}}}{2}$或$\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{5}$ | D. | $\frac{{\sqrt{3}}}{2}$或$\sqrt{5}$ |
分析 根据题意,由等比数列的性质计算可得m=±4,分2种情况讨论:当m=4时,圆锥曲线${x^2}+\frac{y^2}{4}=1$表示椭圆,当m=-4时,圆锥曲线${x^2}-\frac{y^2}{4}=1$表示双曲线,分别求出此时的离心率,综合可得答案.
解答 解:根据题意,m是两个正数2,8的等比中项,则有m2=2×8=16,
解可得m=±4,
当m=4时,圆锥曲线${x^2}+\frac{y^2}{4}=1$表示椭圆,
其中a=2,b=1,
则c=$\sqrt{{a}^{2}-{b}^{2}}$=$\sqrt{3}$,
其离心率e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$;
当m=-4时,圆锥曲线${x^2}-\frac{y^2}{4}=1$表示双曲线,
其中a=1,b=2,
则c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{5}$,
其离心率e=$\frac{c}{a}$=$\sqrt{5}$;
则其离心率为$\frac{\sqrt{3}}{2}$或$\sqrt{5}$;
故选:D.
点评 本题考查椭圆.双曲线的几何性质,注意m的取值可正可负,要分2种情况讨论.


 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a∈[0,6] | B. | $a∈[-\sqrt{6},\sqrt{6}]$ | C. | a∈[-6,6] | D. | a∈[1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| 储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-2,2] | C. | [-2,1] | D. | [-1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
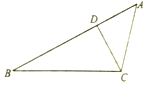 如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.
如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com