
【题目】已知函数![]() .
.
(1)若![]() 是实数集
是实数集![]() 上的奇函数,求
上的奇函数,求![]() 的值;
的值;
(2)用定义证明![]() 在实数集
在实数集![]() 上单调递增;
上单调递增;
(3)若![]() 值域为
值域为![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】试题分析:(1)根据奇函数性质f(x)+f(﹣x)= 0,化简可得![]() 的值;(2)关键在于作差之后的变形,一般先通分再因式分解,最后讨论各因子符号,进而确定差的符号(3)先根据函数单调性确定函数值域,再根据集合包含关系,利用数轴确定
的值;(2)关键在于作差之后的变形,一般先通分再因式分解,最后讨论各因子符号,进而确定差的符号(3)先根据函数单调性确定函数值域,再根据集合包含关系,利用数轴确定![]() 的取值范围.
的取值范围.
试题解析:(1)∵f(x)是R上的奇函数,
∴f(x)+f(﹣x)=m﹣![]() +m﹣
+m﹣![]() =0,即2m﹣(
=0,即2m﹣( ![]() +
+![]() )=02m﹣1=0,
)=02m﹣1=0,
解得m=![]() ;
;
(2)设 x1<x2且x1,x2∈R,
则f(x1)﹣f(x2)=m﹣![]() ﹣(m﹣
﹣(m﹣![]() )=
)=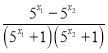 ,
,
∵x1<x2∴![]() ,
, ![]() ,
,
∴f(x1)﹣f(x2)<0,即f(x1)<f(x2),
∴f(x)在R上单调递增;
(3)由![]()
![]() ,所以m﹣1<f(x)<m,f(x)值域为D,且
,所以m﹣1<f(x)<m,f(x)值域为D,且![]()
∴D=(m﹣1,m),
∵![]()
∴,
![]() ∴m的取值范围是
∴m的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上且以2为周期的偶函数,当0≤x≤1时,f(x)=x2.如果函数g(x)=f(x)-(x+m)有两个零点,则实数m的值为( )
A.2k(k∈Z) B.2k或2k+![]() (k∈Z)
(k∈Z)
C.0 D.2k或2k-![]() (k∈Z)
(k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABCA1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,AA1=12,点D是AB的中点.
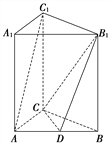
(1)求证:AC⊥B1C;
(2)求证:AC1∥平面CDB1.
查看答案和解析>>
科目:高中数学 来源: 题型:
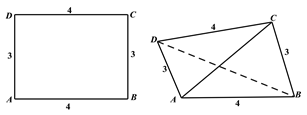
【题目】已知矩形![]() 的长
的长![]() ,宽
,宽![]() ,将其沿对角线
,将其沿对角线![]() 折起,得到四面体
折起,得到四面体![]() ,
,
如图所示,给出下列结论:
①四面体![]() 体积的最大值为
体积的最大值为![]() ;
;
②四面体![]() 外接球的表面积恒为定值;
外接球的表面积恒为定值;
③若![]() 分别为棱
分别为棱![]() 的中点,则恒有
的中点,则恒有![]() 且
且![]() ;
;
④当二面角![]() 为直二面角时,直线
为直二面角时,直线![]() 所成角的余弦值为
所成角的余弦值为![]() ;
;
⑤当二面角![]() 的大小为
的大小为![]() 时,棱
时,棱![]() 的长为
的长为![]() .
.
其中正确的结论有____________________(请写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂今年1月、2月、3月生产某种产品的数量分别是1万件、2万件、1.3万件,为了预测以后每个月的产量,以这三个月的产品数量为依据,用一个函数模拟该产品的月产量y与月份x的关系,模拟函数可以选用二次函数或函数y=abx+c(其中a,b,c为常数),已知4月份该产品的产量为1.37万件,请问用以上哪个函数作为模拟函数较好?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信是现代生活进行信息交流的重要工具,若要调查某公司使用微信的员工经常使用微信与年龄的关系,并规定每天使用微信时间在一小时以上为经常使用微信。据统计,该公司200名员工中90%的人使用微信,其中不经常使用微信的有60人,其余经常使用微信。若将员工年龄分成青年(年龄小于40岁)和中年(年龄不小于40岁)两个阶段,使用微信的中75%是青年人.经常使用微信的员工中,有80人是青年人.
(1)请完成如下![]() 联列表,
联列表,
青年人 | 中年人 | 合计 | |
经常使用微信 | |||
不经常使用微信 | |||
合计 |
(2)由列联表中所得数据,是否有99.9%的把握认为“经常使用微信与年龄有关”?
(3)现采用分层抽样的方法从“经常使用微信的人”中抽取6人,从已抽取的这6人中任选2人,求“选出的2人均为青年人”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+cx+d(a≠0)是R上的奇函数,当x=1时,f(x)取得极值-2.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调区间和极大值;
(3)证明:对任意x1、x2∈(-1,1),不等式|f(x1)-f(x2)|<4恒成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com