
分析 (I)由题意可得$\left\{\begin{array}{l}{m-2>0}\\{7-m>0}\\{m-2≠7-m}\end{array}\right.$,解出即可得出.
(II)当m=6时,椭圆方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1,则△ABF2周长L=|AB|+|AF2|+|BF2|=4a.
解答 解:(I)由题意可得$\left\{\begin{array}{l}{m-2>0}\\{7-m>0}\\{m-2≠7-m}\end{array}\right.$,
解得2<m<7,且m$≠\frac{9}{2}$.
(II)当m=6时,椭圆方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1,
∴以a2=4,即a=2.
则△ABF2周长L=|AB|+|AF2|+|BF2|=|AF1|+|BF1|+|AF2|+|BF2|=4a=8.
点评 本题考查了椭圆的标准方程及其性质,考查了推理能力与计算能力,属于中档题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:选择题
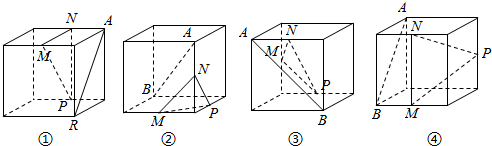
| A. | ①② | B. | ②④ | C. | ①③ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “π是函数y=sinx的一个周期”或“2π是函数y=cosx的一个周期” | |
| B. | “x2+y2=0”是“xy=0”的必要不充分条件 | |
| C. | “若a≤b,则2a≤2b-1”的否命题 | |
| D. | “?a∈(0,+∞),函数y=ax在定义域内单调递增”的否定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com