
【题目】某次测验,将20名学生平均分为两组,测验结果两组学生成绩的平均分和标准差分别为90,6;80,4.则这20名学生成绩的方差为_____.
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
平面直角坐标系![]() 中,射线
中,射线![]() :
:![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的方程为
的方程为![]() ;以原点为极点,
;以原点为极点,![]() 轴的非负半轴为极轴建立极坐标系.曲线
轴的非负半轴为极轴建立极坐标系.曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出射线![]() 的极坐标方程以及曲线
的极坐标方程以及曲线![]() 的普通方程;
的普通方程;
(Ⅱ)已知射线![]() 与
与![]() 交于
交于![]() ,
,![]() ,与
,与![]() 交于
交于![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级的全体学生平均分成![]() 个小组,且每个小组均有
个小组,且每个小组均有![]() 名男生和多名女生.现从各个小组中随机抽取一名同学参加社区服务活动,若抽取的
名男生和多名女生.现从各个小组中随机抽取一名同学参加社区服务活动,若抽取的![]() 名学生中至少有一名男生的概率为
名学生中至少有一名男生的概率为![]() ,则( )
,则( )
A.该班级共有![]() 名学生
名学生
B.第一小组的男生甲被抽去参加社区服务的概率为![]()
C.抽取的![]() 名学生中男女生数量相同的概率是
名学生中男女生数量相同的概率是![]()
D.设抽取的![]() 名学生中女生数量为
名学生中女生数量为![]() ,则
,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将![]() 方格表任意一个角上的
方格表任意一个角上的![]() 小方格表挖去,剩下的图形称为“角形”.现在
小方格表挖去,剩下的图形称为“角形”.现在![]() 方格表中放置一些两两不重叠的角形,要求角形的边界与方格表的边界或分格线重合.求正整数
方格表中放置一些两两不重叠的角形,要求角形的边界与方格表的边界或分格线重合.求正整数![]() 的最大值,使得无论以何种方式放置了
的最大值,使得无论以何种方式放置了![]() 个角形之后,总能在方格表中再放入一个完整的角形.
个角形之后,总能在方格表中再放入一个完整的角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着科技的发展,网购已经逐渐融入了人们的生活.在家里面不用出门就可以买到自己想要的东西,在网上付款即可,两三天就会送到自己的家门口,如果近的话当天买当天就能送到,或者第二天就能送到,所以网购是非常方便的购物方式.某公司组织统计了近五年来该公司网购的人数![]() (单位:人)与时间
(单位:人)与时间![]() (单位:年)的数据,列表如下:
(单位:年)的数据,列表如下:
| 1 | 2 | 3 | 4 | 5 |
| 24 | 27 | 41 | 64 | 79 |
(1)依据表中给出的数据,是否可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(计算结果精确到0.01).(若
并加以说明(计算结果精确到0.01).(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式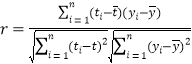
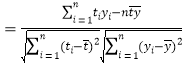 ,参考数据
,参考数据![]() .
.
(2)建立![]() 关于
关于![]() 的回归方程,并预测第六年该公司的网购人数(计算结果精确到整数).
的回归方程,并预测第六年该公司的网购人数(计算结果精确到整数).
(参考公式: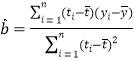
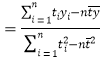 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 在线段
在线段![]() 上运动,则下列判断中正确的是( )
上运动,则下列判断中正确的是( )

①平面![]() 平面
平面![]() ;
;
②![]() 平面
平面![]() ;
;
③异面直线![]() 与
与![]() 所成角的取值范围是
所成角的取值范围是![]() ;
;
④三棱锥![]() 的体积不变.
的体积不变.
A. ①② B. ①②④ C. ③④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线![]() .以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线M的极坐标方程为
.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线M的极坐标方程为![]() .
.
(1)求C的极坐标方程和曲线M的直角坐标方程;
(2)若M与C只有1个公共点P,求m的值与P的极坐标(![]() ,
,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】港珠澳大桥是中国建设史上里程最长,投资最多,难度最大的跨海桥梁项目,大桥建设需要许多桥梁构件。从某企业生产的桥梁构件中抽取![]() 件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间
件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.

(1)求这些桥梁构件质量指标值落在区间![]() 内的频率;
内的频率;
(2)若将频率视为概率,从该企业生产的这种桥梁构件中随机抽取![]() 件,记这
件,记这![]() 件桥梁构件中质量指标值位于区间
件桥梁构件中质量指标值位于区间![]() 内的桥梁构件件数为
内的桥梁构件件数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的是( )
A.将一组数据中的每一个数据都加上或减去同一个常数后,方差不变
B.设有一个线性回归方程![]() ,变量x增加1个单位时,y平均增加5个单位
,变量x增加1个单位时,y平均增加5个单位
C.设具有相关关系的两个变量x,y的相关系数为r,则![]() 越接近于0,x和y之间的线性相关程度越强
越接近于0,x和y之间的线性相关程度越强
D.在一个![]() 列联表中,由计算得
列联表中,由计算得![]() 的值,则
的值,则![]() 的值越大,判断两个变量间有关联的把握就越大
的值越大,判断两个变量间有关联的把握就越大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com