
【题目】如图,已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N.
,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N. 
(1)求椭圆C的方程;
(2)求 ![]()
![]() 的最小值;
的最小值;
(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点,求证:|OR||OS|是定值.
【答案】
(1)解:由题意可知:T(﹣2,0),∴a=2.又 ![]() ,a2=b2+c2,
,a2=b2+c2,
联立解得a=2,c= ![]() ,b=1.
,b=1.
∴椭圆C的方程为 ![]() =1
=1
(2)解:设M(x0,y0),N(x0,﹣y0).
把点M的坐标代入椭圆方程可得: ![]() =1﹣
=1﹣ ![]() .
.
![]()
![]() =
= ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() ,
,
∵﹣2<x0<2,
∴当且仅当x0=﹣ ![]() 时,
时, ![]()
![]() 取得最小值﹣
取得最小值﹣ ![]()
(3)证明:设P(x1,y1),
直线MP的方程为:y﹣y1= ![]() (x﹣x1),
(x﹣x1),
令y=0,可得xR= ![]() ,
,
同理可得:xS= ![]() ,
,
∵点M,P都在椭圆上,
∴ ![]() =4
=4 ![]() ,
, ![]() =4
=4 ![]() ,
,
∴:|OR||OS|=xRxS= ![]() =
= ![]() =4是定值
=4是定值
【解析】(1)由题意可知:T(﹣2,0),a=2.又 ![]() ,a2=b2+c2 , 联立解出即可得出.(2)设M(x0 , y0),N(x0 , ﹣y0).把点M的坐标代入椭圆方程可得:
,a2=b2+c2 , 联立解出即可得出.(2)设M(x0 , y0),N(x0 , ﹣y0).把点M的坐标代入椭圆方程可得: ![]() =1﹣
=1﹣ ![]() .利用数量积运算性质可得:
.利用数量积运算性质可得: ![]()
![]() =
= ![]() ﹣
﹣ ![]() ,﹣2<x0<2,再利用二次函数的单调性即可得出.(3)设P(x1 , y1),直线MP的方程为:y﹣y1=
,﹣2<x0<2,再利用二次函数的单调性即可得出.(3)设P(x1 , y1),直线MP的方程为:y﹣y1= ![]() (x﹣x1),令y=0,可得xR , 同理可得:xS , 利用点M,P都在椭圆上,及其|OR||OS|=xRxS即可证明.
(x﹣x1),令y=0,可得xR , 同理可得:xS , 利用点M,P都在椭圆上,及其|OR||OS|=xRxS即可证明.


 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】下列结论正确的是( )
A.各个面都是三角形的几何体是三棱锥
B.一平面截一棱锥得到一个棱锥和一个棱台
C.棱锥的侧棱长与底面多边形的边长相等,则该棱锥可能是正六棱锥
D.圆锥的顶点与底面圆周上的任意一点的连线都是母线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点(1, ![]() )是函数f(x)=
)是函数f(x)= ![]() ax(a>0,a≠1)图象上一点,等比数列{an}的前n项和为c﹣f(n).数列{bn}(bn>0)的首项为2c,前n项和满足
ax(a>0,a≠1)图象上一点,等比数列{an}的前n项和为c﹣f(n).数列{bn}(bn>0)的首项为2c,前n项和满足 ![]() =
= ![]() +1(n≥2). (Ⅰ)求数列{an}的通项公式;
+1(n≥2). (Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{ ![]() }的前n项和为Tn , 问使Tn>
}的前n项和为Tn , 问使Tn> ![]() 的最小正整数n是多少?
的最小正整数n是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,若不等式f(﹣2m2+2m﹣1)+f(8m+ek)>0(e是自然对数的底数),对任意的m∈[﹣2,4]恒成立,则整数k的最小值是( )
,若不等式f(﹣2m2+2m﹣1)+f(8m+ek)>0(e是自然对数的底数),对任意的m∈[﹣2,4]恒成立,则整数k的最小值是( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|﹣1≤x<3},B={x|2x﹣4≤x﹣2}.
(1)求A∩(UB);
(2)若函数f(x)=lg(2x+a)的定义域为集合C,满足AC,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组检测数据![]() ,如下表所示:
,如下表所示:
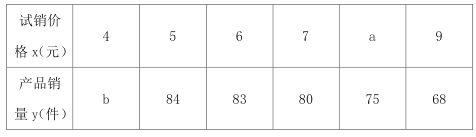
已知变量![]() 具有线性负相关关系,且
具有线性负相关关系,且![]() ,
, ![]() ,现有甲、乙、丙三位同学通过计算求得其回归直线方程分别为:甲
,现有甲、乙、丙三位同学通过计算求得其回归直线方程分别为:甲![]() ;乙
;乙![]() ;丙
;丙![]() ,其中有且仅有一位同学的计算结果是正确的.
,其中有且仅有一位同学的计算结果是正确的.
(1)试判断谁的计算结果正确?并求出![]() 的值;
的值;
(2)若由线性回归方程得到的估计数据与检测数据的误差不超过1,则该检测数据是“理想数据”,现从检测数据中随机抽取2个,求这两个检测数据均为“理想数据”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个函数f(x)和g(x)的定义域和值域都是集合{1,2,3},其定义如下表:则方程g(f(x))=x的解集为( )
x | 1 | 2 | 3 |
f(x) | 2 | 3 | 1 |
x | 1 | 2 | 3 |
g(x) | 3 | 2 | 1 |
A.{1}
B.{2}
C.{3}
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com