
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,讨论
时,讨论![]() 的单调性;
的单调性;
(3)若![]() 有两个极值点
有两个极值点![]() 、
、![]() ,且不等式
,且不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)见解析(3)
(2)见解析(3)![]()
【解析】
(1)先对函数求导,求出切线方程的斜率,再求出该点的函数值,利用点斜式求解;(2)利用导函数的正负判断原函数的单调性,再分类讨论;(3)从函数![]() 在
在![]() 上有两个极值点,根据韦达定理得到
上有两个极值点,根据韦达定理得到![]() 与
与![]() 的关系,分离出参数
的关系,分离出参数![]() ,从而得到关于
,从而得到关于![]() 的新函数,再求最值.
的新函数,再求最值.
解:(1)当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以,函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() ;
;
(2)函数![]() 定义域为
定义域为![]() ,
,![]() ,
,
二次函数![]() 的判别式
的判别式![]() .
.
①若![]() 时,即当
时,即当![]() 时,对任意的
时,对任意的![]() ,
,![]() ,
,
此时,函数![]() 单调递增区间为
单调递增区间为![]() ,无减区间;
,无减区间;
②若![]() 时,即当
时,即当![]() 时,
时,
由![]() ,得
,得![]() 或
或![]() .
.
当![]() ,或
,或![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
此时,函数![]() 单调递增区间为
单调递增区间为 ,
,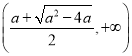 ,单调递减区间为
,单调递减区间为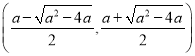 ;
;
(3)由(2)知,![]() ,且
,且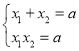 ,
,
不等式![]() 恒成立等价于
恒成立等价于![]() 恒成立,
恒成立,
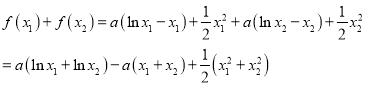
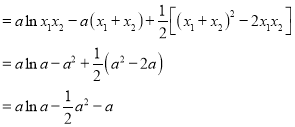
所以![]() ,
,
令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,所以
,所以![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() .
.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
【题目】微博橙子辅导用简单随机抽样方法抽取了100名同学,对其社会实践次数进行调查,结果如下:

若将社会实践次数不低于12次的学生称为“社会实践标兵”.
(1)将频率视为概率,估计该校1600名学生中“社会实践标兵”有多少人?
(2)从已抽取的8名“社会实践标兵”中随机抽取4位同学参加社会实践表彰活动.
(ⅰ)设A为事件"抽取的4位同学中既有男同学又有女同学”,求事件A发生的概率;
(ⅱ)用X表示抽取的“社会实践标兵”中男生的人数,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为![]() (t为参数,0).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数,0).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(Ⅰ)写出曲线C的直角坐标方程;
(Ⅱ)若直线l与曲线C交于A,B两点,且AB的长度为2![]() ,求直线l的普通方程.
,求直线l的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为满足人民群众便利消费、安全消费、放心消费的需求,某社区农贸市场管理部门规划建造总面积为![]() 的新型生鲜销售市场.市场内设蔬菜水果类和肉食水产类店面共80间.每间蔬菜水果类店面的建造面积为
的新型生鲜销售市场.市场内设蔬菜水果类和肉食水产类店面共80间.每间蔬菜水果类店面的建造面积为![]() ,月租费为
,月租费为![]() 万元;每间肉食水产店面的建造面积为
万元;每间肉食水产店面的建造面积为![]() ,月租费为0.8万元.全部店面的建造面积不低于总面积的80%,又不能超过总面积的85%.①两类店面间数的建造方案为_________种.②市场建成后所有店面全部租出,为保证任何一种建设方案平均每间店面月租费不低于每间蔬菜水果类店面月租费的90%,则
,月租费为0.8万元.全部店面的建造面积不低于总面积的80%,又不能超过总面积的85%.①两类店面间数的建造方案为_________种.②市场建成后所有店面全部租出,为保证任何一种建设方案平均每间店面月租费不低于每间蔬菜水果类店面月租费的90%,则![]() 的最大值为_________万元.
的最大值为_________万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() 的值;
的值;
(2)证明:当![]() 时,
时,![]() 在
在![]() 上有两个极值点;
上有两个极值点;
(3)设![]() ,若
,若![]() 在
在![]() 上是单调减函数(
上是单调减函数(![]() 为自然对数的底数),求实数
为自然对数的底数),求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司准备上市一款新型轿车零配件,上市之前拟在其一个下属4S店进行连续30天的试销.定价为1000元/件.试销结束后统计得到该4S店这30天内的日销售量(单位:件)的数据如下表:
日销售量 | 40 | 60 | 80 | 100 |
频数 | 9 | 12 | 6 | 3 |
(1)若该4S店试销期间每个零件的进价为650元/件,求试销连续30天中该零件日销售总利润不低于24500元的频率;
(2)试销结束后,这款零件正式上市,每个定价仍为1000元,但生产公司对该款零件不零售,只提供零件的整箱批发,大箱每箱有60件,批发价为550元/件;小箱每箱有45件,批发价为600元/件.该4S店决定每天批发两箱,根据公司规定,当天没销售出的零件按批发价的9折转给该公司的另一下属4S店.假设该4店试销后的连续30天的日销售量(单位:件)的数据如下表:
日销售量 | 50 | 70 | 90 | 110 |
频数 | 5 | 15 | 8 | 2 |
(ⅰ)设该4S店试销结束后连续30天每天批发两大箱,这30天这款零件的总利润;
(ⅱ)以总利润作为决策依据,该4S店试销结束后连续30天每天应该批发两大箱还是两小箱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年,新型冠状病毒引发的疫情牵动着亿万人的心,八方驰援战疫情,众志成城克时难,社会各界支援湖北共抗新型冠状病毒肺炎,重庆某医院派出3名医生,2名护士支援湖北,现从这5人中任选2人定点支援湖北某医院,则恰有1名医生和1名护士被选中的概率为( )
A.0.7B.0.4C.0.6D.0.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,直线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,且c(sinC-sinA)=(sinA+sinB) (b - a).
(1)求B;
(2)若c=8,点M,N是线段BC的两个三等分点,![]() ,求AM的值.
,求AM的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com