已知二次函数f(x)=ax2+bx+c和“伪二次函数”g(x)=ax2+bx+clnx(a、b、c∈R,abc≠0),
(I)证明:只要a<0,无论b取何值,函数g(x)在定义域内不可能总为增函数;
(Ⅱ)在二次函数f(x)=ax2+bx+c图象上任意取不同两点A(x1,y1),B(x2,y2),线段AB中点的横坐标为x,记直线AB的斜率为k,(i)求证:k=f′(x);(ii)对于“伪二次函数”g(x)=ax2+bx+clnx,是否有(i)同样的性质?证明你的结论.
【答案】
分析:(I)利用导数判断函数的单调性,证明函数g(x)在定义域内不可能总为增函数;
(Ⅱ)根据定义,利用导数的运算求k,并证明“伪二次函数”g(x)=ax
2+bx+clnx,是否有(i)同样的性质.
解答:解:(I)函数的定义域为(0,+∞),要使函数g(x)在定义域内总为增函数,
则
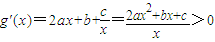
恒成立,①--------(1分)
当x>0时恒成立,则2ax
2+bx+c>0 ②
因为a<0,由二次函数的性质,②不可能恒成立.
则函数g(x)不可能总为增函数.--------(4分)
(II)(i)
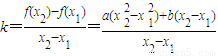
=a(x
2+x
1)+b=2ax
+b,--------(6分)
由f'(x)=2ax+b,所以f'(x
)=2ax
+b,…..(7分)
则k=f′(x
).--------(7分)
(ii)不妨设x
2>x
1,对于“伪二次函数”:g(x)=ax
2+bx+clnx,
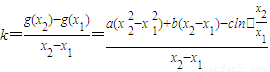
=
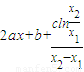
,③--------(9分)
由(ⅰ)中①知
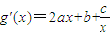
,
如果有(ⅰ)的性质,则g'(x
)=k,④,
比较③④两式得
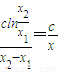
,c≠0,
即:
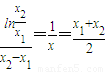
--------(12分)
不妨令
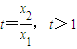
,则
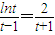
,即
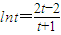
⑤,
设
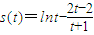
,则
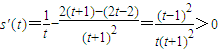
,
∴s(t)在(1,+∞)上递增,∴s(t)>s(1)=0.
∴⑤式不可能成立,④式不可能成立,即g'(x
)≠k.--------(14分)
∴“伪二次函数”g(x)=ax
2+bx+clnx,不具有(ⅰ)的性质.--------(15分)
点评:本题主要考查了利用导数研究函数的性质,综合性较强,运算量较大.

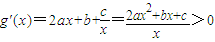 恒成立,①--------(1分)
恒成立,①--------(1分)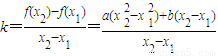 =a(x2+x1)+b=2ax+b,--------(6分)
=a(x2+x1)+b=2ax+b,--------(6分)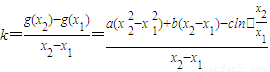 =
=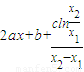 ,③--------(9分)
,③--------(9分)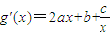 ,
,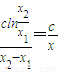 ,c≠0,
,c≠0,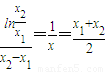 --------(12分)
--------(12分)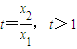 ,则
,则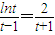 ,即
,即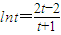 ⑤,
⑤,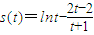 ,则
,则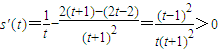 ,
,
