
(1)m为何值时,y的极小值是0?
(2)求证:不论m是什么数值,函数的图象(即抛物线)的顶点都在同一条直线l1上.
(3)平行于l1的直线中,哪些与抛物线相交,哪些不相交?求证:任一条平行于l1而与抛物线相交的直线,被各抛物线截出的线段都相等.
(1)解:用配方法得y=(x+![]() )2-
)2-![]() ,
,
∴y的极小值为-![]() .
.
由-![]() =0,得m=-
=0,得m=-![]() ,即当m=-
,即当m=-![]() 时,y的极小值是0.
时,y的极小值是0.
(2)证明:函数图象抛物线的顶点坐标为(-![]() ,-
,-![]() ),
),
即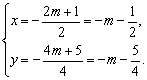 (x、y为顶点的两坐标)
(x、y为顶点的两坐标)
两式相减得x-y=![]() ,此即各抛物线顶点坐标所满足的方程,它的图形是一条直线.方程中不含m,因此,不论m是什么值,抛物线的顶点都在这条直线l1:x-y=
,此即各抛物线顶点坐标所满足的方程,它的图形是一条直线.方程中不含m,因此,不论m是什么值,抛物线的顶点都在这条直线l1:x-y=![]() 上.
上.
(3)设l:x-y=a为任一条平行于l1的直线,
由![]()
消去y,得x2+2mx+m2-1+a=0,即(x+m)2=1-a.
当1-a≥0,即a≤1时,直线l与抛物线相交,而1-a<0,即a>1时,直线l与抛物线不相交.
若a≤1,则x=-m±![]() ,即x1=-m-
,即x1=-m-![]() ,x2=-m+
,x2=-m+![]() .
.
∴x2-x1=2![]() .
.
直线l被抛物线截得的线段AB的长为
|AB|=![]() |x2-x1|=
|x2-x1|=![]() ·2
·2![]() =2
=2![]() 与m无关.
与m无关.
因而直线l被各抛物线截出的线段都相等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com