
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() =2.71828……是自然对数的底数),曲线
=2.71828……是自然对数的底数),曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行.
轴平行.
(1)求![]() 的值;
的值;
(2)求![]() 的单调区间;
的单调区间;
(3)设![]() ,其中
,其中![]() 是
是![]() 的导函数.证明:对任意
的导函数.证明:对任意![]() >0,
>0,![]() <
<![]() .
.
【答案】(1)![]() ;(2)单调递增区间为
;(2)单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题分析:(1)求出函数的导函数,函数在点![]() 处的切线与
处的切线与![]() 轴平行,说明
轴平行,说明![]() ,则可得
,则可得![]() ;(2)求出函数的定义域,然后让导数等于
;(2)求出函数的定义域,然后让导数等于![]() ,求出极值点,借助于导函数在各区间内的符号求函数
,求出极值点,借助于导函数在各区间内的符号求函数![]() 的单调区间;(3)
的单调区间;(3)![]() ,分别研究
,分别研究![]() 的单调性,可得函数的范围,即可证明结论.
的单调性,可得函数的范围,即可证明结论.
试题解析:(1)由![]() ,得
,得![]() ,
,![]() ,由于曲线
,由于曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行,所以
轴平行,所以![]() ,因此
,因此![]()
(2)由(1)得![]() ,令
,令![]() 当
当![]() 时,
时, ![]() ;当
;当![]() 时,
时,![]() .又
.又![]() ,所以
,所以![]() 时,
时,![]() ;
;
![]() 时,
时,![]() ,因此
,因此![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(3)证明因为![]() ,所以
,所以![]() ,
,![]() .因此对任意
.因此对任意![]() 等价于
等价于![]() .
.
由(2)知![]() ,
,
所以![]() ,
,
因此当![]() 时,
时,![]() ﹥0,
﹥0, ![]() 单调递增;当
单调递增;当![]() 时,
时, ![]() ﹤0,
﹤0, ![]() 单调递减.
单调递减.
所以![]() 的最大值为
的最大值为![]() 故
故![]() . 设
. 设![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() ﹥0,
﹥0, ![]() 单调递增,
单调递增, ![]() ﹥
﹥![]() ,
,
故![]() 时,
时,![]() ,即
,即![]() ﹥1.所以
﹥1.所以![]() ﹤
﹤![]() ,
,
因此对任意![]() ,
, ![]() ﹤
﹤![]() .
.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(-2,2),函数g(x)=f(x-1)+f(3-2x).
(1)求函数g(x)的定义域;
(2)若f(x)是奇函数,且在定义域上单调递减,求不等式g(x)≤0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,在多面体![]() 中,
中,![]() ⊥平面
⊥平面![]() ,
,![]() ,且
,且![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() ,
,![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
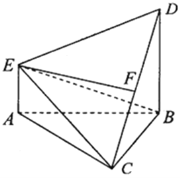
(1)若![]() 是线段
是线段![]() 的中点,证明:
的中点,证明:![]() ⊥面
⊥面![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=x+![]() 有如下性质:如果常数t>0,那么该函数在(0,
有如下性质:如果常数t>0,那么该函数在(0, ![]() ]上是减函数,在[
]上是减函数,在[![]() ,+∞)上是增函数.
,+∞)上是增函数.
(1)已知f(x)=![]() ,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域;
,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域;
(2)对于(1)中的函数f(x)和函数g(x)=-x-2a,若对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】5名男生4名女生站成一排,求满足下列条件的排法:
(1)女生都不相邻有多少种排法?
(2)男生甲、乙、丙排序一定(只考虑位置的前后顺序),有多少种排法?
(3)男甲不在首位,男乙不在末位,有多少种排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在△ABC中,三条边![]() 所对的角分别为A、B,C,向量
所对的角分别为A、B,C,向量![]() =(
=(![]() ),
),![]() =(
=(![]() ),且满足
),且满足![]()
![]() =
=![]() .
.
(1)求角C的大小;
(2)若sinA,sinC,sinB成等比数列,且![]() =﹣8,求边
=﹣8,求边![]() 的值并求△ABC外接圆的面积.
的值并求△ABC外接圆的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com