
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①,若p∨q为真命题,则p、q至少一个为真命题,则p∧q也不一定为真命题;
②,“x>5”⇒“x2-4x-5>0”;“x2-4x-5>0”⇒“x>5或x<-1“;
③,命题:?x∈R,2x>x2的否定为:?x0∈R,2${\;}^{{x}_{0}}$≤x02;
④,当x=0,ex=1+x.
解答 解:对于①,若p∨q为真命题,则p、q至少一个为真命题,则p∧q也不一定为真命题,故错;
对于②,“x>5”⇒“x2-4x-5>0”;“x2-4x-5>0”⇒“x>5或x<-1“,故正确;
对于③,命题:?x∈R,2x>x2的否定为:?x0∈R,2${\;}^{{x}_{0}}$≤x02,故错;
对于④,当x=0,ex=1+x,故正确.
故选:B
点评 本题考查了命题真假的判定,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
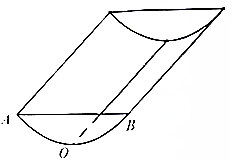 某小区内有一条形状如图的沟渠,沟沿是两条平行线段,沟渠宽AB为20厘米,沟渠的直截面ABO为一段抛物线,抛物线顶点为O,对称轴与地面垂直,沟渠深20厘米,沟渠中水深10厘米.
某小区内有一条形状如图的沟渠,沟沿是两条平行线段,沟渠宽AB为20厘米,沟渠的直截面ABO为一段抛物线,抛物线顶点为O,对称轴与地面垂直,沟渠深20厘米,沟渠中水深10厘米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | [0,2] | C. | (0,2) | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | $[0,\frac{{\sqrt{2}}}{2})$ | C. | $(0,\frac{{\sqrt{2}}}{2}]$ | D. | $[\frac{{\sqrt{2}}}{2},\sqrt{2}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com