
| 偏爱蔬菜 | 偏受肉类 | 合计 | |
| 五十岁以下 | |||
| 五十岁以上 | |||
| 合计 |
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
分析 (1)根据12位五十岁以下的亲友中有4位偏爱蔬菜:18位五十岁以上的亲友中有2位偏爱肉类,从而可得列联表;
(2)利用列联表,计算K2,与临界值比较,可得结论;
(3)由(2)可知其亲友的饮食习惯与年龄有很大关系,故宜采用分层抽样的方法
解答 解:(1)2×2的列联表:
| 偏爱蔬菜 | 偏爱肉类 | 合计 | |
| 50岁以下 | 4 | 8 | 12 |
| 50岁以上 | 16 | 2 | 18 |
| 合计 | 20 | 10 | 30 |
点评 本题考查概率与统计知识,考查分层抽样,考查学生的计算能力,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. | 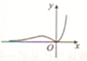 | C. | 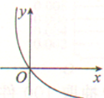 | D. | 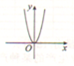 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\root{n-m}{\frac{{b}^{n}}{{a}^{m}}}$ | B. | $\frac{{b}^{n}-{a}^{m}}{n-m}$ | C. | $\root{n-m}{{b}^{n}-{a}^{m}}$ | D. | $\frac{\frac{{b}^{n}}{{a}^{m}}}{n-m}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
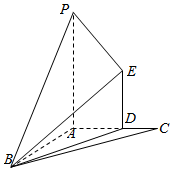 平面外ABC的一点P,AP、AB、AC两两互相垂直,过AC的中点D做ED⊥面ABC,且ED=1,PA=2,AC=2,连接BP,BE,多面体B-PADE的体积是$\frac{\sqrt{3}}{3}$;
平面外ABC的一点P,AP、AB、AC两两互相垂直,过AC的中点D做ED⊥面ABC,且ED=1,PA=2,AC=2,连接BP,BE,多面体B-PADE的体积是$\frac{\sqrt{3}}{3}$;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com