
【题目】已知函数 ![]() ,现有一组数据(数据量较大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分)
,现有一组数据(数据量较大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分) 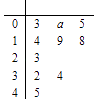
(Ⅰ)现从茎叶图的数据中任取4个数据分别替换m的值,
求至少有2个数据使得函数f(x)没有零点的概率;
(Ⅱ)以频率估计概率,若从该组数据中随机抽取4个数据分别替换m的值,记使得函数f(x)没有零点的个数为ξ,求ξ的分布列及数学期望.
【答案】解:(Ⅰ)根据茎叶图中的数据,计算平均数为 ![]() =
= ![]() ×(0.3+0.1×a+0.5+1.4+1.9+1.8+2.3+3.2+3.4+4.5)=2,
×(0.3+0.1×a+0.5+1.4+1.9+1.8+2.3+3.2+3.4+4.5)=2,
解得a=7;
从茎叶图10个数据中任取4个,有 ![]() =210种不同的取法;
=210种不同的取法;
函数f(x)=x2+ ![]() 中,
中,
△=2(m﹣1)2﹣m=2m2﹣5m+2,
令△<0,解得 ![]() <m<2,
<m<2,
∴满足函数f(x)没有零点的数据是0.7,1.4,1.8,1.9共4个;
用抽出的4个数分别替换m的值,至少有2个数据使得函数f(x)没有零点的概率为
P=1﹣ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
(Ⅱ)满足函数f(x)没有零点的数据有4个,
∴ξ的所有可能取值分别为0,1,2,3,4;
则P(ξ=0)= ![]() =
= ![]() ,
,
P(ξ=1)= ![]() =
= ![]() ,
,
P(ξ=2)= ![]() =
= ![]() ,
,
P(ξ=3)= ![]() =
= ![]() ,
,
P(ξ=4)= ![]() =
= ![]() ;
;
∴ξ的分布列为:
ξ | 0 | 1 | 2 | 3 | 4 |
P | | | | | |
数学期望为Eξ=0× ![]() +1×
+1× ![]() +2×
+2× ![]() +3×
+3× ![]() +4×
+4× ![]() =
= ![]() =1.6
=1.6
【解析】(Ⅰ)根据茎叶图中的数据,利用平均数的定义列方程求出a的值;利用判别式△<0求出函数f(x)没有零点时m的取值范围,再利用对立事件的概率公式计算所求的概率值;(Ⅱ)根据题意知ξ的所有可能取值,求出对应的概率,写出ξ的分布列,计算数学期望值.
【考点精析】关于本题考查的茎叶图和离散型随机变量及其分布列,需要了解茎叶图又称“枝叶图”,它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少;在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能得出正确答案.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣1.
(1)对于任意的1≤x≤2,不等式4m2|f(x)|+4f(m)≤|f(x﹣1)|恒成立,求实数m的取值范围;
(2)若对任意实数x1∈[1,2].存在实数x2∈[1,2],使得f(x1)=|2f(x2)﹣ax2|成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以“赏中华诗词,寻文化基因,品生活之美”为宗旨的《中国诗词大会》,是央视科教频道推出的一档大型演播室文化益智节目,每季赛事共分为10场,每场分个人追逐赛与擂主争霸赛两部分,其中擂主争霸赛在本场个人追逐赛的优胜者与上一场擂主之间进行,一共备有9道抢答题,选手抢到并答对获得1分,答错对方得1分,当有一个选手累计得分达到5分时比赛结束,该选手就是本场的擂主,在某场比赛中,甲、乙两人进行擂主争霸赛,设每个题目甲答对的概率都为 ![]() ,乙答对的概率为
,乙答对的概率为 ![]() ,每道题目都有人抢答,且每人抢到答题权的概率均为
,每道题目都有人抢答,且每人抢到答题权的概率均为 ![]() ,各题答题情况互不影响. (Ⅰ)求抢答一道题目,甲得1分的概率;
,各题答题情况互不影响. (Ⅰ)求抢答一道题目,甲得1分的概率;
(Ⅱ)现在前5题已经抢答完毕,甲得2分,乙得3分,在接下来的比赛中,设甲的得分为ξ,求ξ的分布列及数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD与正方形BCEF所成角的二面角的平面角的大小是 ![]() ,PQ是正方形BDEF所在平面内的一条动直线,则直线BD与PQ所成角的取值范围是( )
,PQ是正方形BDEF所在平面内的一条动直线,则直线BD与PQ所成角的取值范围是( ) 
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|ax2+x﹣4a|,其中x∈[﹣2,2],a∈[﹣1,1].
(1)当α=1时,求函数y=f(x)的值域;
(2)记f(x)的最大值为M(a),求M(a)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且λSn=λ﹣an , 其中λ≠0且λ≠﹣1.
(1)证明:{an}是等比数列,并求其通项公式;
(2)若 ![]() ,求λ.
,求λ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人上午7时,乘摩托艇以匀速vkm/h(8≤v≤40)从A港出发到距100km的B港去,然后乘汽车以匀速wkm/h(30≤w≤100)自B港向距300km的C市驶去.应该在同一天下午4至9点到达C市. 设乘坐汽车、摩托艇去目的地所需要的时间分别是xh,yh.
(1)作图表示满足上述条件的x,y范围;
(2)如果已知所需的经费p=100+3(5﹣x)+2(8﹣y)(元),那么v,w分别是多少时p最小?此时需花费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com