
分析 先根据[$\frac{f(x)}{x}$]′=$\frac{xf′(x)-f(x)}{{x}^{2}}$>0判断函数$\frac{f(x)}{x}$的单调性,进而分别看x>1和0<x<1时f(x)与0的关系,再根据函数的奇偶性判断-1<x<0和x<-1时f(x)与0的关系,最后取x的并集即可得到答案.
解答 解:[$\frac{f(x)}{x}$]′=$\frac{xf′(x)-f(x)}{{x}^{2}}$>0,即x>0时$\frac{f(x)}{x}$是增函数,
当x>1时,$\frac{f(x)}{x}$>f(1)=0,f(x)>0.
0<x<1时,$\frac{f(x)}{x}$<f(1)=0,f(x)<0,
又f(x)是奇函数,所以-1<x<0时,f(x)=-f(-x)>0,
x<-1时f(x)=-f(-x)<0,
则不等式x2f(x)>0即f(x)>0的解集是(-1,0)∪(1,+∞),
故答案为:(-1,0)∪(1,+∞).
点评 本题主要考查了函数单调性与奇偶性的应用.在判断函数的单调性时,常可利用导函数来判断.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3f(2)<2f(3) | B. | 3f(2)>2f(3) | C. | 2f(2)<3f(3) | D. | 2f(2)>3f(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
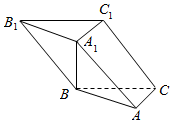 如图,在斜三棱柱ABC-A1B1C1中,A1B⊥AC,且A1B=AC=5,AA1=BC=13,且AB=12.
如图,在斜三棱柱ABC-A1B1C1中,A1B⊥AC,且A1B=AC=5,AA1=BC=13,且AB=12.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB是圆O的直径,C为AB的延长线上一点,切线CD交圆O于点D,∠ACD的平分线分别交DB,DA于点E,F.
如图,AB是圆O的直径,C为AB的延长线上一点,切线CD交圆O于点D,∠ACD的平分线分别交DB,DA于点E,F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com