
(07年湖北卷理)(14分)
已知![]() 为正整数,
为正整数,
(I)用数学归纳法证明:当![]() 时,
时,![]() ;
;
(II)对于![]() ,已知
,已知![]() ,求证:
,求证:![]() ,
,![]() ;
;
(III)求出满足等式![]() 的所有正整数
的所有正整数![]() .
.
本小题主要考查数学归纳法、数列求和、不等式等基础知识和基本的运算技能,考查分析问题能力和推理能力.
解析:解法1:(Ⅰ)证:用数学归纳法证明:
()当![]() 时,原不等式成立;当
时,原不等式成立;当![]() 时,左边
时,左边![]() ,右边
,右边![]() ,
,
因为![]() ,所以左边
,所以左边![]() 右边,原不等式成立;
右边,原不等式成立;
()假设当![]() 时,不等式成立,即
时,不等式成立,即![]() ,则当
,则当![]() 时,
时,
![]() ,
,![]() ,于是在不等式
,于是在不等式![]() 两边同乘以
两边同乘以![]() 得
得
![]() ,
,
所以![]() .即当
.即当![]() 时,不等式也成立.
时,不等式也成立.
综合()()知,对一切正整数![]() ,不等式都成立.
,不等式都成立.
(Ⅱ)证:当![]() 时,由(Ⅰ)得
时,由(Ⅰ)得![]() ,
,
于是![]()
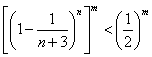 ,
,![]() .
.
(Ⅲ)解:由(Ⅱ)知,当![]() 时,
时,
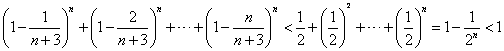 ,
,
![]() .
.
即![]() .即当
.即当![]() 时,不存在满足该等式的正整数
时,不存在满足该等式的正整数![]() .
.
故只需要讨论![]() 的情形:
的情形:
当![]() 时,
时,![]() ,等式不成立;
,等式不成立;
当![]() 时,
时,![]() ,等式成立;
,等式成立;
当![]() 时,
时,![]() ,等式成立;
,等式成立;
当![]() 时,
时,![]() 为偶数,而
为偶数,而![]() 为奇数,故
为奇数,故![]() ,等式不成立;
,等式不成立;
当![]() 时,同
时,同![]() 的情形可分析出,等式不成立.
的情形可分析出,等式不成立.
综上,所求的![]() 只有
只有![]() .
.
解法2:(Ⅰ)证:当![]() 或
或![]() 时,原不等式中等号显然成立,下用数学归纳法证明:
时,原不等式中等号显然成立,下用数学归纳法证明:
当![]() ,且
,且![]() 时,
时,![]() ,
,![]() . ①
. ①
()当![]() 时,左边
时,左边![]() ,右边
,右边![]() ,因为
,因为![]() ,所以
,所以![]() ,即左边
,即左边![]() 右边,不等式①成立;
右边,不等式①成立;
()假设当![]() 时,不等式①成立,即
时,不等式①成立,即![]() ,则当
,则当![]() 时,
时,
因为![]() ,所以
,所以![]() .又因为
.又因为![]() ,所以
,所以![]() .
.
于是在不等式![]() 两边同乘以
两边同乘以![]() 得
得
![]() ,
,
所以![]() .即当
.即当![]() 时,不等式①也成立.
时,不等式①也成立.
综上所述,所证不等式成立.
(Ⅱ)证:当![]() ,
,![]() 时,
时,![]() ,
,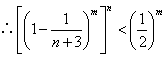 ,
,
而由(Ⅰ),![]() ,
,
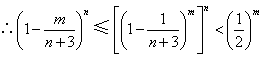 .
.
(Ⅲ)解:假设存在正整数![]() 使等式
使等式![]() 成立,
成立,
即有 . ②
. ②
又由(Ⅱ)可得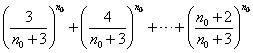
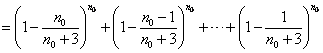
![]() ,与②式矛盾.
,与②式矛盾.
故当![]() 时,不存在满足该等式的正整数
时,不存在满足该等式的正整数![]() .
.
下同解法1.


科目:高中数学 来源: 题型:
(07年湖北卷理)已知直线![]() (
(![]() 是非零常数)与圆
是非零常数)与圆![]() 有公共点,且公共点的横坐标和纵坐标均为整数,那么这样的直线共有( )
有公共点,且公共点的横坐标和纵坐标均为整数,那么这样的直线共有( )
A.60条 B.66条 C.72条 D.78条
查看答案和解析>>
科目:高中数学 来源: 题型:
(07年湖北卷理)已知直线![]() (
(![]() 是非零常数)与圆
是非零常数)与圆![]() 有公共点,且公共点的横坐标和纵坐标均为整数,那么这样的直线共有( )
有公共点,且公共点的横坐标和纵坐标均为整数,那么这样的直线共有( )
A.60条 B.66条 C.72条 D.78条
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com