
【题目】已知椭圆![]() 的短轴长为2,离心率为
的短轴长为2,离心率为![]()
(1)求椭圆C的方程;
(2)设过点M(2,0)的直线l与椭圆C相交于A,B两点,F1为椭圆的左焦点.
①若B点关于x轴的对称点是N,证明:直线AN恒过一定点;
②试求椭圆C上是否存在点P,使F1APB为平行四边形?若存在,求出F1APB的面积,若不存在,请说明理由.
【答案】(1)定点![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由短轴长和离心率可以求得![]() ,从而得到椭圆的方程.(2)设出
,从而得到椭圆的方程.(2)设出![]() ,则直线
,则直线![]() 的方程为:
的方程为: ![]() ,利用
,利用![]() 在直线
在直线![]() 上,直线
上,直线![]() 的方程又可以转化为
的方程又可以转化为![]() ,联立方程组
,联立方程组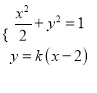 并消去
并消去![]() ,利用韦达定理把直线
,利用韦达定理把直线![]() 的方程化简为
的方程化简为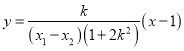 ,从而得到直线过定点
,从而得到直线过定点![]() .(3)中设出
.(3)中设出![]() ,因
,因![]() 、
、![]() 互相平分,故可用
互相平分,故可用![]() 表示
表示![]() ,最后利用
,最后利用![]() 在椭圆上求出
在椭圆上求出![]() 的大小,从而求出平行四边形的面积.
的大小,从而求出平行四边形的面积.
解析:(1)∵椭圆![]() 的短轴长为2,∴
的短轴长为2,∴![]() ,解得
,解得![]() ,∵离心率为
,∵离心率为![]() ,∴
,∴![]() ,解得
,解得![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .
.
(2)证明:①设过![]() 的直线
的直线![]() ,联立
,联立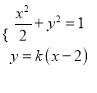 ,得
,得![]() ,∵直线与椭圆交于两点,∴
,∵直线与椭圆交于两点,∴![]() ,即
,即![]() .
.
设![]() ,则
,则![]() ,∵
,∵![]() 点关于
点关于![]() 轴的对称点是
轴的对称点是![]() ,∴
,∴![]() .设直线
.设直线![]() ,∵
,∵![]() 满足直线
满足直线![]() ,∴
,∴![]()
![]()
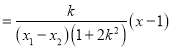 ,∴直线
,∴直线![]() 过定点
过定点![]() .
.
(2)椭圆左焦点![]() ,设
,设![]() 的中点
的中点![]() ,则
,则![]() ,
, ![]() ,假设存在点
,假设存在点![]() 使
使![]() 为平行四边形,则
为平行四边形,则![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
, ![]() ,即
,即![]() ,∵
,∵![]() 在椭圆
在椭圆![]() 上,∴
上,∴![]() .整理得
.整理得![]() ,解得
,解得![]() 或
或![]() (舍),此时,
(舍),此时, 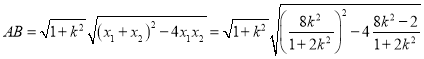
![]()
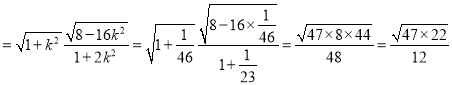
左焦点![]() 直线
直线![]() 的距离
的距离![]() ,∴平行四边形
,∴平行四边形![]() 的面积
的面积![]() .
.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+ ![]() +2﹣2a(a>0)的图象在点(1,f(1))处的切线与直线y=2x+1平行.
+2﹣2a(a>0)的图象在点(1,f(1))处的切线与直线y=2x+1平行.
(1)求a,b满足的关系式;
(2)若f(x)≥2lnx在[1,+∞)上恒成立,求a的取值范围;
(3)证明:1+ ![]() +
+ ![]() +…+
+…+ ![]() >
> ![]() (2n+1)+
(2n+1)+ ![]() (n∈N*).
(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将一副三角板拼接,使它们有公共边BC,且使两个三角形所在的平面互相垂直,若
∠BAC=90°,AB=AC,∠CBD=90°,∠BDC=60°,BC=6。

⑴ 求证:平面![]() 平面ACD;
平面ACD;
⑵ 求二面角![]() 的平面角的正切值;
的平面角的正切值;
⑶ 设过直线AD且与BC平行的平面为![]() ,求点B到平面
,求点B到平面![]() 的距离。
的距离。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是偶函数.
是偶函数.
(1)求证:![]() 是偶函数;
是偶函数;
(2)求证:![]() 在
在![]() 上是增函数;
上是增函数;
(3)设![]() (
(![]() ,且
,且![]() ),若对任意的
),若对任意的![]() ,在区间
,在区间![]() 上总存在两个不同的数
上总存在两个不同的数![]() ,
,![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲、乙两地某月14时的气温情况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:
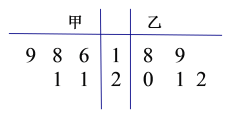
①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的平均气温的标准差小于乙地该月14时的平均气温的标准差;
④甲地该月14时的平均气温的标准差大于乙地该月14时的平均气温的标准差,
其中根据茎叶图能得到的统计结论的编号为( )
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信是现代生活进行信息交流的重要工具,据统计,某公司![]() 名员工中
名员工中![]() 的人使用微信,其中每天使用微信时间在一小时以内的有
的人使用微信,其中每天使用微信时间在一小时以内的有![]() 人,其余每天使用微信在一小时以上.若将员工年龄分成青年(年龄小于
人,其余每天使用微信在一小时以上.若将员工年龄分成青年(年龄小于![]() 岁)和中年(年龄不小于
岁)和中年(年龄不小于![]() 岁)两个阶段,使用微信的人中
岁)两个阶段,使用微信的人中![]() 是青年人.若规定:每天使用微信时间在一小时以上为经常使用微信,经常使用微信的员工中
是青年人.若规定:每天使用微信时间在一小时以上为经常使用微信,经常使用微信的员工中![]() 是青年人.
是青年人.
(Ⅰ)若要调查该公司使用微信的员工经常使用微信与年龄的关系,列出![]() 列联表;
列联表;
青年人 | 中年人 | 合计 | |
经常使用微信 | |||
不经常使用微信 | |||
合计 |
(Ⅱ)由列联表中所得数据,是否有![]() 的把握认为“经常使用微信与年龄有关”?
的把握认为“经常使用微信与年龄有关”?
(Ⅲ)采用分层抽样的方法从“经常使用微信”的人中抽取![]() 人,从这
人,从这![]() 人中任选
人中任选![]() 人,求事件
人,求事件![]() “选出的
“选出的![]() 人均是青年人”的概率.
人均是青年人”的概率.
附:
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 在第一象限内的点
在第一象限内的点![]() 到焦点
到焦点![]() 的距离为
的距离为![]() .
.
(1)若![]() ,过点
,过点![]() ,
, ![]() 的直线
的直线![]() 与抛物线相交于另一点
与抛物线相交于另一点![]() ,求
,求![]() 的值;
的值;
(2)若直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,与圆
两点,与圆![]() 相交于
相交于![]() 两点,
两点, ![]() 为坐标原点,
为坐标原点, ![]() ,试问:是否存在实数
,试问:是否存在实数![]() ,使得
,使得![]() 的长为定值?若存在,求出
的长为定值?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com