
【题目】如图所示,在直角梯形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 上的点,
上的点,![]() ,且
,且![]() (如图1). 将四边形
(如图1). 将四边形![]() 沿
沿![]() 折起,连结
折起,连结![]() (如图2). 在折起的过程中,下列说法中错误的个数是( )
(如图2). 在折起的过程中,下列说法中错误的个数是( )
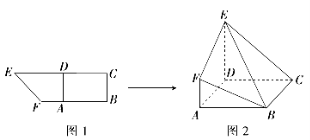
①![]() 平面
平面![]() ;
;
②![]() 四点不可能共面;
四点不可能共面;
③若![]() ,则平面
,则平面![]() 平面
平面![]() ;
;
④平面![]() 与平面
与平面![]() 可能垂直.
可能垂直.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】(1)求经过直线l1:2x+3y-5=0与l2:7x+15y+1=0的交点,且平行于直线x+2y-3=0的直线方程;
(2)求与直线3x+4y-7=0垂直,且与原点的距离为6的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 为圆
为圆![]() 上的动点,定点
上的动点,定点![]() ,线段
,线段![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]() .
.
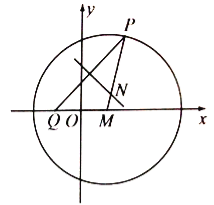
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)记动点![]() 的轨迹为曲线
的轨迹为曲线 ![]() ,设圆
,设圆![]() 的切线
的切线![]() 交曲线
交曲线![]() 于
于![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“银发浪潮”的涌来,养老是当下普遍关注的热点和难点问题,某市创新性的采用“公建民营”的模式,建立标准的“日间照料中心”,既吸引社会力量广泛参与养老建设,也方便规范化管理,计划从中抽取5个中心进行评估,现将所有中心随机编号,用系统(等距)抽样的方法抽取,已知抽取到的号码有5号23号和29号,则下面号码中可能被抽到的号码是( )
A. 9 B. 12 C. 15 D. 17
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为2,
的边长为2,![]() 分别为线段
分别为线段![]() 的中点,在五棱锥
的中点,在五棱锥![]() 中,
中,![]() 为棱
为棱![]() 的中点,平面
的中点,平面![]() 与棱
与棱![]() 分别交于点
分别交于点![]() .
.
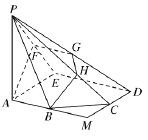
(1)求证:![]() ;
;
(2)若![]() 底面
底面![]() ,且
,且![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
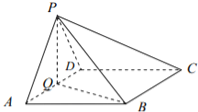
(1)若PA=PD,求证:平面PQB⊥平面PAD;
(2)若平面PAD⊥平面ABCD,且PA=PD=AD=2,点M在线段PC上,且PM=3MC,求三棱锥P﹣QBM的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com