
【题目】已知椭圆![]() 的焦距为2,点
的焦距为2,点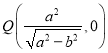 在直线
在直线![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 为坐标原点,
为坐标原点, ![]() 为直线
为直线![]() 上一动点,过点
上一动点,过点![]() 作直线与椭圆相切点于点
作直线与椭圆相切点于点![]() ,求
,求![]() 面积
面积![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)利用椭圆![]()
![]() 的焦距为2,点
的焦距为2,点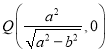 在直线
在直线![]() 上,求出
上,求出![]() ,
, ![]() ,
, ![]() ,即可求椭圆
,即可求椭圆![]() 的标准方程;(2)设出切线方程和代入椭圆方程,求得关于
的标准方程;(2)设出切线方程和代入椭圆方程,求得关于![]() 的一元二次方程,
的一元二次方程, ![]() ,求得,求得
,求得,求得![]() 和
和![]() 的关系,根据三角形的面积公式将面积
的关系,根据三角形的面积公式将面积![]() 表示为关于
表示为关于![]() 的函数,
的函数,
利用导数可求得其最小值.
试题解析:(1)椭圆![]()
![]() 的焦距为2,
的焦距为2, ![]()
![]() ,又点
,又点 在直线
在直线![]() 上,
上, ![]()
![]() ,
, ![]()
![]() .故椭圆
.故椭圆![]() 的标准方程是
的标准方程是![]() .
.
(2)由题意直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
, ![]() .
.
由![]() 得
得![]() ,相切
,相切![]() ,
,
![]()
![]() ,且
,且![]() ,
, ![]() ,
, ![]() .
.![]()
![]() ,
, ![]()
![]() .
.
当![]() 时,
时, ![]() ,又
,又![]() ,
, ![]() ,
, ![]()
![]() .
.
令![]()
![]() ,则
,则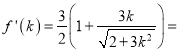
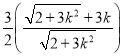 ,
,
由![]() 得
得![]() ,
, ![]() 在
在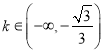 上单减,在
上单减,在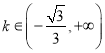 单增,
单增,
![]()
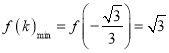 .即当
.即当![]() 的斜率为
的斜率为![]() 时,
时, ![]() 面积
面积![]() 的最小值为
的最小值为![]() .
.
同理当![]() 时,
时, ![]() ,当
,当![]() 的斜率为
的斜率为![]() 时,
时, ![]() 面积
面积![]() 的最小值为
的最小值为![]() .
.
综上, ![]() 面积
面积![]() 的最小值为
的最小值为![]() .
.


科目:高中数学 来源: 题型:
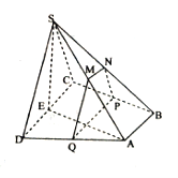
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 分别为
分别为![]() 的中点,
的中点, ![]() 为
为![]() 的中点,过
的中点,过![]() 作平面
作平面![]() 分别与交
分别与交![]() 于点
于点![]() .
.
(Ⅰ)当![]() 为
为![]() 中点时,求证:平面
中点时,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加数学竞赛培训,在培训期间他们参加的5次预寒成绩记录如下:
甲:82,82,79,95,87
乙:95,75,80,90,85
(1)用茎叶图表示这两组数据;
(2)求甲、乙两人成绩的平均数与方差;
(3)若现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适,说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中__________为真命题(把所有真命题的序号都填上).
①“![]() ”成立的必要条件是“
”成立的必要条件是“![]() ”;
”;
②“若![]() 成等差数列,则
成等差数列,则![]() ”的否命题;
”的否命题;
③“已知数列![]() 的前
的前![]() 项和为
项和为![]() ,若数列
,若数列![]() 是等比数列,则
是等比数列,则![]() 成等比数列.”的逆否命题;
成等比数列.”的逆否命题;
④“已知![]() 是
是![]() 上的单调函数,若
上的单调函数,若![]() ,则
,则![]() ”的逆命题.
”的逆命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn满足2Sn=an+1﹣2n+1+1,n∈N* , 且a1 , a2+5,a3成等差数列.
(1)求a1的值;
(2)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】教育学家分析发现加强语文乐队理解训练与提高数学应用题得分率有关,某校兴趣小组为了验证这个结论,从该校选择甲乙两个同轨班级进行试验,其中甲班加强阅读理解训练,乙班常规教学无额外训练,一段时间后进行数学应用题测试,统计数据情况如下面的![]() 列联表(单位:人)
列联表(单位:人)

(1)能够据此判断有97.5%把握热内加强语文阅读训练与提高数学应用题得分率有关?
(2)经过多次测试后,小明正确解答一道数学应用题所用的时间在5—7分钟,小刚正确解得一道数学应用题所用的时间在6—8分钟,现小明、小刚同时独立解答同一道数学应用题,求小刚比小明现正确解答完的概率;
(3)现从乙班成绩优秀的8名同学中任意抽取两人,并对他们点答题情况进行全程研究,记A、B两人中被抽到的人数为X,求X的分布列及数学期望E(X).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}中,a2﹣a1=2,且2a2为3a1和a3的等差中项.
(1)求数列{an}的通项公式;
(2)设bn=2log3an+1,且数列{ ![]() }的前n项和为Tn . 求Tn .
}的前n项和为Tn . 求Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com