
 箱中有3个黑球,6个白球,每个球被取到的概率相同,
箱中有3个黑球,6个白球,每个球被取到的概率相同,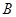 箱中没有球.我们把从
箱中没有球.我们把从 箱中取1个球放入
箱中取1个球放入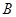 箱中,然后在
箱中,然后在 箱中补上1个与取走的球完全相同的球,称为一次操作,这样进行三次操作.
箱中补上1个与取走的球完全相同的球,称为一次操作,这样进行三次操作.
(1)分别求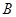 箱中恰有1个、2个、3个白球的概率;
箱中恰有1个、2个、3个白球的概率;
(2)从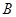 箱中一次取出2个球,记白球的个数为
箱中一次取出2个球,记白球的个数为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:杭州一模 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:
已知甲在A箱内放有6个球(3个红球,1个黑球,2个黄球),乙在B箱内放有6个球(a个红球,b个黑球,c个黄球,a、b、c∈N*).现分别从A、B箱中分别取出1个球(假设每球等可能取出),当取出球的颜色如下列情形时,乙胜.
甲取球 | 红 | 黄 | 黑 |
乙取球 | 红或黄 | 黄 | 黑 |
(1)用a、b表示乙获胜的概率;
(2)当a、b为何值时,乙获胜的概率最大,并求此最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com