
分析 讨论a的取值:a=0,容易判断满足条件;a>0时,要满足条件,a便满足$\frac{1}{a}$≥10;a<0时,能判断f(x)的对称轴$\frac{1}{a}$<1,从而满足条件,这样这三种情况所得a的范围求并集即可得出实数a的取值范围.
解答 解:①若a=0,则f(x)=-2x+1,满足在区间[1,10]上单调递减;
②若a>0,f(x)的对称轴为x=$\frac{1}{a}$,f(x)在[1,10]上单调递减,则:$\frac{1}{a}$≥10,
∴0<a≤$\frac{1}{10}$;
③若a<0,则f(x)的对称轴x=$\frac{1}{a}$<1,满足f(x)在[1,10]上单调递减;
∴综上得实数a的取值范围是$({-∞,\frac{1}{10}}]$,
故答案为$({-∞,\frac{1}{10}}]$.
点评 考查二次函数的对称轴,二次函数的单调性,不要漏了a=0的情况.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{3},\frac{1}{2}})$ | B. | $({\frac{1}{3},\frac{1}{2}})∪({1,+∞})$ | C. | (1,+∞) | D. | $({\frac{1}{3},1})∪({1,+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
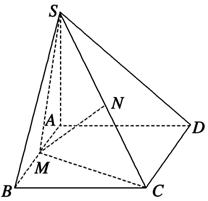 如图所示,在四棱锥S-ABCD中,AD∥BC,AD⊥AB,CD⊥平面SAD,SA=AD=2,AB=1,SB=$\sqrt{5}$,SD=2$\sqrt{2}$,M,N分别为AB,SC的中点.
如图所示,在四棱锥S-ABCD中,AD∥BC,AD⊥AB,CD⊥平面SAD,SA=AD=2,AB=1,SB=$\sqrt{5}$,SD=2$\sqrt{2}$,M,N分别为AB,SC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-3<x<0或x>3} | B. | {x|x<-3或0<x<3} | C. | {x|x<-3或x>3} | D. | {x|-3<x<0或0<x<3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com